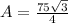Question

Find the area of the region common to r=5 and r=10sin(θ). Enter an exact answer.

Answer 1

The correct exact area of the region common to r=5 and r=10sin(θ) is
`(75 √(3))/(4)`

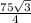
To find the area of the region common to r=5 and r=10sin(θ), we need to set these two equations equal to each other and find the values of θ where they intersect.

5=10sin(θ)

Divide both sides by 10:

sin(θ)= 1/2

This occurs when θ= π/6 or θ= 5π/6 (and their coterminal angles).

Now, set up the integral to find the area between the curves:

`A=(1)/(2) \int_(\theta_1)^(\theta_2)\left[r_2(\theta)^2-r_1(\theta)^2\right] d \theta`

In this case,
`r_2(\theta)=10 \sin (\theta) \text { and } r_1(\theta)=5 \text { : }`

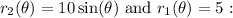
`\begin{aligned}& A=(1)/(2) \int_(\theta_1)^(\theta_2)\left[(10 \sin (\theta))^2-5^2\right] d \theta \\& A=(1)/(2) \int_(\theta_1)^(\theta_2)\left[100 \sin ^2(\theta)-25\right] d \theta\end{aligned}`

`A=(1)/(2) \int_(\theta_1)^(\theta_2) 75-75 \cos (2 \theta) d \theta`

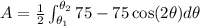
Now, integrate:

​
`A=(1)/(2)\left[75 \theta-(75)/(2) \sin (2 \theta)\right]_(\theta_1)^(\theta_2)`

Evaluate at the upper and lower limits:

`A=(1)/(2)\left[(75 \theta_2)/(2)-(75)/(2) \sin \left(2 \theta_2\right)-(75 \theta_1)/(2)+(75)/(2) \sin \left(2 \theta_1\right)\right]`

Now, use the values
`\theta_1=(\pi)/(6) \text { and } \theta_2=(5 \pi)/(6):`

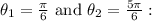
`A=(1)/(2)\left[(75 \pi)/(2)-(75)/(2) \sin \left((5 \pi)/(3)\right)-(75 \pi)/(2)+(75)/(2) \sin \left((\pi)/(3)\right)\right]`

Simplify the above equation:

`A=(1)/(2)\left[(75 \pi)/(2)+(75 √(3))/(4)-(75 \pi)/(2)+(75 √(3))/(4)\right]`

Combine like terms:

`A=(75 √(3))/(4)`