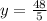Question

The straight line L_(1) passes through the points with coordinates (4,6) and (12,2) The straight line L_(2) passes through the origin and has gradient -3 The lines L_(1) and L_(2) intersect at point P. Find the coordinates of P.

Answer 1

`P=(-(16)/(5) ,(48)/(5) )`

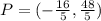
Step-by-step explanation:

equation of L_(1):

`(y-y1)/(y2-y1) = (x-x1)/(x2-x1)`

`(y-6)/(2-6) =(x-4)/(12-4)`

`(y-6)/(-4) =(x-4)/(8)`

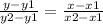
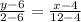
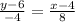
8(y - 6) = -4(x - 4)

-2(y - 6) = x - 4

-2y + 12 = x - 4

x + 2y = 16 ... [1]

equation of L_(2):

`y-y1=m(x-x1)`

y - 0 = -3(x - 0)

y = -3x

3x + y = 0 ... [2]

[1] & [2]

x + 2y = 16 ⇔ x + 2y = 16

3x + y = 0 ⇔ 6x + 2y = 0

------------------ (-)

-5x = 16

x =
`-(16)/(5)`

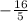
[2]

3x + y = 0

`3(-(16)/(5) ) + y =0`

`y=(48)/(5)`