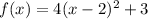Question

Let f(x) = a(x - h)^(2)+ k. The vertex of the graph of f is at (2,3) and the graph passes through (1,7). Find the values of h, k, and a.

Answer 1

Answers:

• a = 4
• h = 2
• k = 3

==============================================

Work Shown:

The vertex is (2,3) which means h = 2 pairs up with k = 3

The parabola also passes through (1,7). So x = 1 pairs up with y = f(x) = 7

We'll use these four values to determine the value of 'a'

`f(x) = a(x-h)^2+k\\\\f(x) = a(x-2)^2+3\\\\7 = a(1-2)^2+3\\\\7 = a(-1)^2+3\\\\7 = a(1)+3\\\\7 = a+3\\\\a = 7-3\\\\a = 4`

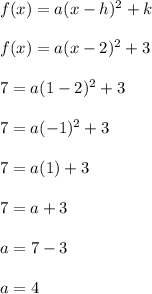
Summary:

• a = 4
• h = 2
• k = 3

The function
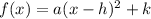`f(x) = a(x-h)^2+k` turns into
`f(x) = 4(x-2)^2+3`