Question

Determine the vapor pressure of an aqueous ethylene glycol (C2H6O2) solution that is 15.7 % C2H6O2 by mass. The vapor pressure of pure water at 25 ∘C is 23.8 torr.

Answer 1

The vapor pressure of the aqueous ethylene glycol solution is approximately 111.4 torr.

To determine the vapor pressure of the aqueous ethylene glycol solution, you can use Raoult's Law, which describes the relationship between the vapor pressure of a solution and the mole fraction of its components.

The formula for Raoult's Law is:

`\[ P_{\text{total}} = P_{\text{A}} \cdot X_{\text{A}} + P_{\text{B}} \cdot X_{\text{B}} \]`

Where:

-
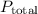`\( P_{\text{total}} \)` is the total vapor pressure of the solution.

-
`\( P_{\text{A}} \) and \( P_{\text{B}} \)` are the vapor pressures of pure components A and B.

-
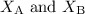`\( X_{\text{A}} \) and \( X_{\text{B}} \)` are the mole fractions of components A and B.

In this case, component A is water and component B is ethylene glycol.

Given:

- Vapor pressure of pure water
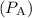`(\( P_{\text{A}} \))` at 25°C = 23.8 torr

- Mass percent of ethylene glycol in the solution = 15.7%

First, calculate the mass percent of water in the solution:

- Mass percent of water = 100% - 15.7% (ethylene glycol)

- Mass percent of water = 84.3%

Now, convert these mass percentages to mole fractions:

- For water:
`\( X_{\text{water}} = \frac{\text{mass percent of water}}{\text{molar mass of water}} \)`

- For ethylene glycol:
`\( X_{\text{ethylene glycol}} = \frac{\text{mass percent of ethylene glycol}}{\text{molar mass of ethylene glycol}} \)`

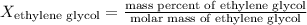
The molar masses are:

- Water (
`H_2O`): 18.015 g/mol

- Ethylene glycol (
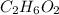`C_2H_6O_2`): 62.07 g/mol

Calculating the mole fractions:

-
`\( X_{\text{water}} = (84.3)/(18.015) \approx 4.68 \)`

-
`\( X_{\text{ethylene glycol}} = (15.7)/(62.07) \approx 0.253 \)`

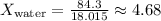
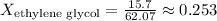
Now, use Raoult's Law to find the total vapor pressure of the solution:

`\[ P_{\text{total}} = P_{\text{water}} \cdot X_{\text{water}} + P_{\text{ethylene glycol}} \cdot X_{\text{ethylene glycol}} \]`

Substitute the given values:

`\[ P_{\text{total}} = 23.8 \, \text{torr} * 4.68 + 0 * 0.253 \]`

`\[ P_{\text{total}} = 111.384 \, \text{torr} \]`