Question

A sample of krypton gas occupies a volume of 7.62 L at 49.0 ∘

C and 0.630 atm. If it is desired to increase the volume of the gas sample to 10.6L, while increasing its pressure to 0.846 atm, the temperature of the gas sample at the new volume and pressure must be ∘
C. 2 more group attempts remaining A 1.41 mol sample of krypton gas is collected at a pressure of 193mmHg and a temperature of 24.0 ∘
C. The volume of the sample is L.

Answer 1

The temperature of the krypton gas sample at the new volume of 10.6 L and pressure of 0.846 atm is 70.5 °C.

Step-by-step explanation:

To find the new temperature, we can use the combined gas law, which relates the initial and final states of a gas sample under changing conditions. The combined gas law is given by the equation:

`\[ (P_1 \cdot V_1)/(T_1) = (P_2 \cdot V_2)/(T_2) \]`

where
`\( P_1 \), \( V_1 \)`, and
`\( T_1 \)` are the initial pressure, volume, and temperature, respectively, and \( P_2 \), \( V_2 \), and \( T_2 \) are the final pressure, volume, and temperature.

In this case, the initial conditions are
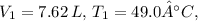`\( V_1 = 7.62 \, L \), \( T_1 = 49.0 °C \),` and
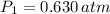`\( P_1 = 0.630 \, atm \)` . The final conditions are
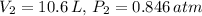`\( V_2 = 10.6 \, L \), \( P_2 = 0.846 \, atm \)`, and we need to find
`\( T_2 \)`.

Rearranging the combined gas law to solve for
`\( T_2 \)`, we get:

`\[ T_2 = (P_2 \cdot V_2 \cdot T_1)/(P_1 \cdot V_1) \]`

Plugging in the values, we find:

`\[ T_2 = ((0.846 \, atm) \cdot (10.6 \, L) \cdot (49.0 °C + 273.15))/((0.630 \, atm) \cdot (7.62 \, L)) \]`

After solving, we get
`\( T_2 \approx 70.5 °C \).`

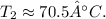
Therefore, the temperature of the krypton gas at the new volume and pressure is approximately 70.5 °C.