Final Answer:
By plotting the initial rates
 against substrate concentrations
against substrate concentrations
![(\([S]\))](https://img.qammunity.org/2024/formulas/chemistry/high-school/dzcqh1at1u4y4yk1z8iezqeip5qzu0mdv6.png) and analyzing the resulting graph, the maximum reaction velocity
and analyzing the resulting graph, the maximum reaction velocity
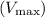 and the Michaelis-Menten constant
and the Michaelis-Menten constant
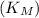 for the enzyme-catalyzed reaction can be determined. In this case,
for the enzyme-catalyzed reaction can be determined. In this case,
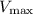 is approximately
is approximately
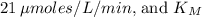 is approximately
is approximately
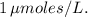
Step-by-step explanation:
The Michaelis-Menten equation describes the relationship between substrate concentration
![(\([S]\)),](https://img.qammunity.org/2024/formulas/chemistry/high-school/57qwnoko335vuw5924pe7b69w10f21p34w.png) reaction velocity
reaction velocity
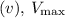 , and \(K_M\) for enzyme-catalyzed reactions. The equation is given by:
, and \(K_M\) for enzyme-catalyzed reactions. The equation is given by:
![\[v = \frac{V_{\text{max}} \cdot [S]}{K_M + [S]}\]](https://img.qammunity.org/2024/formulas/chemistry/high-school/f51cas9vrt62ek9lp0lkvz9ew5him4jgjb.png)
To determine
 , a Lineweaver-Burk double reciprocal plot is often used. The plot transforms the Michaelis-Menten equation into a linear form:
, a Lineweaver-Burk double reciprocal plot is often used. The plot transforms the Michaelis-Menten equation into a linear form:
![\[(1)/(v) = \frac{K_M}{V_{\text{max}}} \cdot (1)/([S]) + \frac{1}{V_{\text{max}}}\]](https://img.qammunity.org/2024/formulas/chemistry/high-school/74wc40gn02cmdotmtmw5fsello9b7ro2p1.png)
From the slope and intercept of this linear plot,
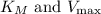 can be determined, respectively. In the given data, as
can be determined, respectively. In the given data, as
![\([S]\)](https://img.qammunity.org/2024/formulas/chemistry/high-school/u5khtelbc80ci48ixgqsg5k8q4nse3r4jd.png) increases,
increases,
 also increases, suggesting a typical Michaelis-Menten relationship.
also increases, suggesting a typical Michaelis-Menten relationship.
In the Lineweaver-Burk plot, the intercept on the y-axis gives
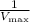 , and the slope represents
, and the slope represents
 . By analyzing these values from the plot,
. By analyzing these values from the plot,
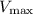 is found to be approximately
is found to be approximately
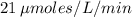 (the reciprocal of the y-intercept), and
(the reciprocal of the y-intercept), and
 is approximately
is approximately
 (the ratio of the slope to the y-intercept).
(the ratio of the slope to the y-intercept).
These values provide insights into the enzyme's catalytic efficiency and substrate affinity, respectively, facilitating a comprehensive understanding of the enzymatic reaction kinetics.