Question

CHAPTER 1 OSCILLATORY MOTION the 10 Practice: A 7-kg mass is hung from the bottom end of a vertical spring fastened to an overhead beam. The mass is set into vertical oscillations having a period of 2.60.s. Find the force constant of the spring.

​

Answer 1

k = 40.9 N/m

Step-by-step explanation:

To find the force constant of the spring, we can use the formula for the period of oscillation of a mass-spring system:

`\boxed{\left\begin{array}{ccc}\text{\underline{Formula for Period:}}\\\\ T = 2 \pi\sqrt{(m)/(k)}\\\\\text{Where:} \\ \bullet \ T \ \text{is the period of oscillation}\\\bullet \ m \ \text{is the mass attached to the spring}\\\bullet \ k \ \text{is the force constant of the spring} \end{array}\right}`

We can rearrange this formula to solve for the force constant, 'k':

`\Longrightarrow T = 2 \pi\sqrt{(m)/(k)}\\\\\\\\\Longrightarrow (T)/(2\pi) = \sqrt{(m)/(k)}\\\\\\\\\Longrightarrow (m)/(k)=\Big((T)/(2\pi)\Big)^2\\ \\ \\\\ \therefore \boxed{k = (4\pi^2m)/(T^2)}`


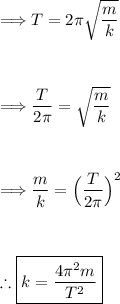
Substitute in the given values:

• m = 7 kg
• T = 2.60 s

`\Longrightarrow k = (4\pi^2(7 \ kg))/((2.60 \ s)^2)\\\\\\\\\therefore \boxed{\boxed{k \approx 40.9 \ (N)/(m) }}`

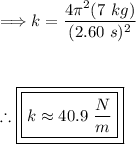
Therefore, the force constant of the spring is approximately 40.9 N/m.