Question

Suppose that a population is growing exponentially and has a doubling time of 5 years, and is currently 1000. Suppose also that there are currently 1000 hats, and hats are being produced at a rate of 200 per year.

(A) Write a function modeling the size of the population.
(B) Write a function modeling the size of the number of hats.
(C) Write a function that models the proportion of people with hats.
(D) Find the rate of change in the proportion of people with hats.
Explain your answers in detail.

Answer 1

(A) models the population growth using exponential growth, (B) models the number of hats with linear increase, (C) models the proportion of people with hats using the given functions, and (D) involves differentiating the proportion function to find the rate of change of the proportion of people with hats.

(A) Modeling the Size of the Population:

Since the population is growing exponentially and has a doubling time of 5 years, we can use the formula for exponential growth:

`P(t)=P 0​ ×2 (t/T)`

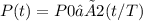
Where:

P(t) is the population at time

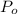`P_(o)` is the initial population (given as 1000).

t is the time in years.

T is the doubling time (given as 5 years).

So, the function modeling the size of the population would be:

P(t)=1000×2 (t/5)

(B) Modeling the Size of the Number of Hats:

The number of hats is increasing by 200 per year. This is a linear increase, so the function modeling the number of hats would be:

H(t)=1000+200t

Where:

H(t) is the number of hats at time

t is the time in years.

(C) Modeling the Proportion of People with Hats:

The proportion of people with hats would be the number of hats divided by the population size:

Proportion(t)= H(t)/P(t)

(D) Finding the Rate of Change in the Proportion of People with Hats:

To find the rate of change of the proportion of people with hats, we need to differentiate the proportion function with respect to time

`d/dt ( H(t)/P(t))`

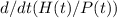
Using the quotient rule for differentiation, the rate of change can be computed.

To summarize, (A) models the population growth using exponential growth, (B) models the number of hats with linear increase, (C) models the proportion of people with hats using the given functions, and (D) involves differentiating the proportion function to find the rate of change of the proportion of people with hats.

For more questions on population growth