2 Answers

← Prev Question Next Question →

Ask a Question

Kaguei Nakueka · Answer 1 · 2024-05-16T20:08:58+0000

Answer:

Look below

Explanation:

Here are the sketches of the given graphs:

Graphs of y = sin(x) and y = sin(x+30°):

The graph of y = sin(x) is a sinusoidal curve that oscillates between -1 and 1 as x varies. It has a period of 2π and crosses the x-axis at integer multiples of π.

The graph of y = sin(x+30°) is obtained by shifting the graph of y = sin(x) to the left by 30°. This shift causes the entire graph to move horizontally to the left by 30°.

Graphs of y = cos(x) and y = cos(x-60°):

The graph of y = cos(x) is also a sinusoidal curve that oscillates between -1 and 1 as x varies. It has a period of 2π and reaches its maximum at x = 0 and its minimum at x = π.

The graph of y = cos(x-60°) is obtained by shifting the graph of y = cos(x) to the right by 60°. This shift causes the entire graph to move horizontally to the right by 60°.

Graphs of y = tan(x) and y = tan(x-45°):

The graph of y = tan(x) is a periodic function with vertical asymptotes at integer multiples of π/2. It has a period of π and increases or decreases indefinitely as x varies.

The graph of y = tan(x-45°) is obtained by shifting the graph of y = tan(x) to the right by 45°. This shift causes the entire graph to move horizontally to the right by 45°.

Wunch · Answer 2 · 2024-05-19T19:25:08+0000

Answer:

Refer to the attachments for the graphs of the given trigonometric functions.

Explanation:

Question 1

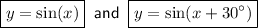
$\boxed{y = \sin(x)}\;\;\textsf{and}\;\;\boxed{y = \sin(x + 30^(\circ))}$

To sketch the graph of y = sin(x), draw a sinusoidal wave that oscillates between y = -1 and y = 1, and passes through the origin.

The graph is continuous and repeats its behavior every 360°.
The minimum value of the graph is -1, which occurs at the troughs of the wave when x = 270° + 360°n (where n is an integer).
The maximum value of the graph is 1, which occurs at the peaks of the wave when x = 90° + 360°n (where n is an integer).
The x-intercepts occur at x = 180°n, where n is an integer.
The y-intercept occurs at the origin (0, 0).

The graph of y = sin(x + 30°) is the parent function y = sin(x) shifted to the left by 30°. The effect of this shift is that the graph will start rising from a point 30° earlier compared to the standard sine wave. This means that:

The minimum value of the graph is -1, which occurs at the troughs of the wave when x = 240° + 360°n (where n is an integer).
The maximum value of the graph is 1, which occurs at the peaks of the wave when x = 60° + 360°n (where n is an integer).
The x-intercepts occur at x = 150° + 180°n, where n is an integer.
The y-intercept occurs at (0, 1/2).

$\hrulefill$

Question 2

$\boxed{y = \cos(x)}\;\;\textsf{and}\;\;\boxed{y = \cos(x - 60^(\circ))}$

To sketch the graph of y = cos(x), draw a sinusoidal wave that oscillates between y = -1 and y = 1.

The graph is continuous and repeats its behavior every 360°.
The minimum value of the graph is -1, which occurs at the troughs of the wave when x = 180° + 360°n (where n is an integer).
The maximum value of the graph is 1, which occurs at the peaks of the wave when x = 360°n (where n is an integer).
The x-intercepts occur at x = 90° + 180°n, where n is an integer.
The y-intercept occurs at (0, 1).

The graph of y = cos(x - 60°) is the parent function y = cos(x) shifted to the right by 60°. The effect of this shift is that the graph will start rising from a point 60° later compared to the standard cos wave. This means that:

The minimum value of the graph is -1, which occurs at the troughs of the wave when x = 240° + 360°n (where n is an integer).
The maximum value of the graph is 1, which occurs at the peaks of the wave when x = 60° + 360°n (where n is an integer).
The x-intercepts occur at x = 150° + 180°n, where n is an integer.
The y-intercept occurs at (0, 1/2).

$\hrulefill$

Question 3

$\boxed{y = \tan(x)}\;\;\textsf{and}\;\;\boxed{y = \tan(x - 45^(\circ))}$

The tangent graph has a distinct shape that is quite different from the sine or cosine graphs. The tangent graph is a periodic function with repeating patterns, but its behavior is more complex due to the nature of the tangent function.

The graph of y = tan(x) has vertical asymptotes at 90° + 180°n, where n is an integer. These asymptotes are vertical lines that the curve gets infinitely close to as it approaches positive or negative infinity, but never touches.