Question

Evaluate the directional derivative of the function f(x,y,z)=6x^(2)y-2z at the point M(7,4,5) in the direction of the vector vec (u)=(1,-2,3).

Answer 1

`\left(-129\, √(14)\right) / 7`.

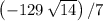Step-by-step explanation:

The directional derivative of
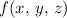`f(x,\, y,\, z)` at the given point in the given direction can be found in the following steps:

• Find the gradient vector
  `\\abla f` by partially differentiating
  `f` with respect to each of the independent variables.
• Substitute in the values of the independent variables at the given position
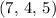  `(7,\, 4,\, 5)` to find the numerical value of vector
  `\Delta f`.
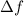• Find the unit vector in the direction of
  `\vec{u}`.
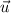• Take the dot product between the unit vector in the direction of
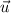  `\vec{u}` and vector
  `\\abla f` to find the directional derivative in the direction
  `\vec{u}\!`.

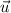For a scalar-valued function
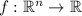`f: \mathbb{R}^(n) \to \mathbb{R}`, the gradient vector
`\\abla f` can be found by partially differentiating this function with respect to each of the independent variables. The dimensionality of this gradient vector would be the same as the number of independent variables required for
`f`. The
`k`th component (
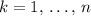`k = 1,\, \dots,\, n`) of this gradient vector would be equal to the partial derivative of
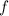`f\!` with respect to the
`k\!`th independent variable.

For example, in this question,
`f(x,\, y,\, z) = 6\, x^(2)\, y - 2\, z` is defined over three independent variables:
`x`,
`y`, and
`z`. Hence, gradient vector
`\\abla f` would be three-dimensional.

Partially differentiate
`f` with respect to the first independent variable
`x` to find the first component of the gradient vector
`\\abla f`:

`\begin{aligned}(\partial f)/(\partial x) &= (\partial)/(\partial x)\left[6\, x^(2) \, y - 2\, z\right] = 6\, (2\, x)\, y = 12\, x\, y\end{aligned}`.

Similarly, partially different
`f` with respect to
`y` and
`z` to find the other two components of
`\\abla f`:

`\begin{aligned}(\partial f)/(\partial y) &= (\partial)/(\partial y)\left[6\, x^(2) \, y - 2\, z\right] = 6\, x^(2)\end{aligned}`.

`\begin{aligned}(\partial f)/(\partial z) &= (\partial)/(\partial z)\left[6\, x^(2) \, y - 2\, z\right] = (-2)\end{aligned}`.

Therefore, the gradient vector of
`f(x,\, y,\, z) = 6\, x^(2)\, y - 2\, z` would be:

`\begin{aligned}\\abla f(x,\, y,\, z) &= \left[\begin{aligned}&(\partial f)/(\partial x) \\ & (\partial f)/(\partial y) \\ &(\partial f)/(\partial z)\end{aligned}\right] = \begin{bmatrix} 12\, x\, y \\ 6\, x^(2) \\ -2\end{bmatrix}\end{aligned}`.

Substitute in the value of
`x`,
`y`, and
`z` at the given position
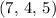`(7,\, 4,\, 5)` to find the numerical value of the gradient vector at that position:

`\begin{aligned}& \\abla f(7,\, 4,\, 5) \\ &= \begin{bmatrix} 12\, x\, y \\ 6\, x^(2) \\ -2\end{bmatrix} = \begin{bmatrix} 12\, (7)\, (4) \\ 6\, (7)^(2) \\ -2\end{bmatrix} = \begin{bmatrix}336 \\ 294 \\ -2\end{bmatrix}\end{aligned}`.

To find the unit vector in the direction of
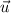`\vec{u}`, divide
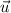`\vec{u}\!` by the magnitude
`\|\vec{u}\|` (a scalar.)

`\begin{aligned}\frac{\vec{u}}{\|\vec{u}\|} &= \frac{1}{\sqrt{1^(2) + (-2)^(2) + 3^(2)}}\, \begin{bmatrix}1 \\ -2 \\ 3\end{bmatrix} \\ &= (1)/(√(14))\, \begin{bmatrix}1 \\ -2 \\ 3\end{bmatrix}\end{aligned}`.

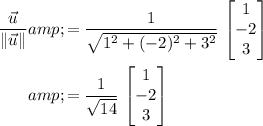To find the directional derivative of function
`f` in the direction
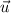`\vec{u}` at the given position, take the vector dot product between:

• the unit vector in the direction of
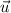  `\vec{u}\!`, and
• the value of
  `\\abla f` at this given position:

`\begin{aligned} D_{\vec{u}} f(7,\, 4,\, 5) &= \frac{\vec{u}}{\|\vec{u}\|}\cdot \\abla f(7,\, 4,\, 5) \\ &= (1)/(√(14))\, \begin{bmatrix}1 \\ -2 \\ 3\end{bmatrix} \cdot \begin{bmatrix}336 \\ 294 \\ -2\end{bmatrix} \\ &= (1)/(√(14))\, \left((1)\, (336) + (-2)\, (294) + (3)\, (-2)\right) \\ &= (-258)/(√(14)) \\ &= -(258\, √(14))/(14) \\ &= -(129\, √(14))/(7)\end{aligned}`.

In other words, the directional derivative of
`f` at
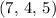`(7,\, 4,\, 5)` in the direction of
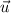`\vec{u}` would be the scalar
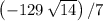`\left(-129\, √(14)\right) / 7`.