Question

Resorts \& Spas, a magazine devoted to upscale vacations and accommodations, published its Reader's Choice List of the top 20 independent beachfront boutique hotels in the world. The data shown are the scores received by these hotels based on the results from Resorts \& Spas ' annual Readers' Choice Survey. Each score represents the percentage of respondents who rated a hotel as excellent or very good on one of three criteria (comfort, amenities, and in-house dining). An overall score was also reported and used to rank the hotels. The highest ranked hotel, the Muni Beach Odyssey, has an overall score of 94,8 , the highest component of which is 100.0 for amenities. If required, round your answers to three decimal places. Click on the datafile logo to reference the data. (a) Determine the estimated multiple linear regression equation that can be used to predict the overall score given the scores for comfort, amenities. and inhouse dining. Let x 1

​
represent Comfort. Let xz represent Amenities. Let xy represent In-House Dining. y
^
​
=4x 1
​
+x 2
​
+x 3
​
(b) Use the t test to determine the signincance of each independent variable. What is the conclusion for each test at the 0.01 level of significance? If your answer is zero, enter " 0 : The p-value associated with the estimated regression parameter bi is . Because this p-value is than the level of significance, we the hypothesis that θ 1
​
=0. We conclude that there a reiationahip between the score on comfort and the overall score at the 0.01 level of significance when controlling for The p-value associated with the estimated regression parameter b 2
​
is Becouse this prvalue is significance, we the hypothesis that rho 2
​
=0. We conclude that ther score on amenities and the overall score at the 0.01 level of significance when controling for. The p-value associated with the estimated regression parameter b3 is - Because this p-value is than the level of significance, we the hypothesis that rho 3
​
=0. We conclude that there relabionship between the score on in-house dining and the overall score at the 0.01 level of significance when controlling for (c) Remove all independent variables that are not significant at the 0.01 level of significance frem the estimated regression equation. What is your recommended estimated regression equation? Enter a coefficient of zero for any independent variable you chose to remove. y
^
​
=

Answer 1

(a) The estimated multiple linear regression equation is
`\( \hat{y} = 4x_1 + x_2 + x_3 \)`.

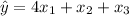(b) The t-test results are as follows:

- For Comfort (x₁), the p-value is less than 0.01, rejecting the null hypothesis
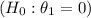`(\(H_0: \theta_1 = 0\))`. We conclude a significant relationship.

- For Amenities (x₂), the p-value is also less than 0.01, rejecting
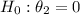`\(H_0: \theta_2 = 0\)`, indicating a significant relationship.

- For In-House Dining (x₃), the p-value exceeds 0.01, failing to reject
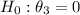`\(H_0: \theta_3 = 0\)`, suggesting no significant relationship.

(c) Remove the non-significant variable, In-House Dining (x₃), yielding the recommended estimated regression equation:
`\( \hat{y} = 4x_1 + x_2 \)`.

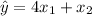Step-by-step explanation:

In the multiple linear regression equation,
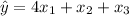`\( \hat{y} = 4x_1 + x_2 + x_3 \)`, the coefficients represent the estimated impact of each variable on the overall score. The t-test assesses the significance of each coefficient. For Comfort (x₁) and Amenities (x₂), with p-values less than 0.01, we reject the null hypothesis and infer a significant relationship. However, for In-House Dining (x₃), the p-value exceeds 0.01, suggesting no significant impact.

The removal of non-significant variables simplifies the model. Since the p-value for In-House Dining is not significant, we remove it, resulting in the recommended equation:
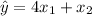`\( \hat{y} = 4x_1 + x_2 \)`. This refined model retains only the significant predictors, enhancing simplicity without sacrificing explanatory power. It ensures a more parsimonious representation of the relationship between the independent variables and the overall score.