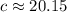Question

Find the missing side and angle measures in triangle ABC. Round your answers to the nearest tenth.

The measure of angle B is approximately
__.

The measure of angle C is approximately
__.

The length of side AB is approximately
___units.

Answer 1

`m\angle B\approx 80.27^\circ\text{ and } m\angle C\approx 59.73^\circ`

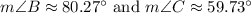
Side AB measures approximately 20.15 units.

Explanation:

We can use the Law of Sines, given by:

`\displaystyle (\sin A)/(a) = (\sin B)/(b) = (\sin C)/(c)`

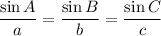
Since we already know ∠A and a, we can use it to determine our other measures.

We know that b is 23. Substitute:

`\displaystyle (\sin 40^\circ)/(15)=(\sin B)/(23)`

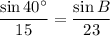
Solve for ∠B:

`\displaystyle \sin B=(23\sin 40^\circ)/(15)`

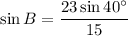
We can take the inverse sine of both sides:

`\displaystyle m\angle B=\sin^(-1)(23\sin 40^\circ)/(15)`

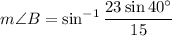
Use a calculator (make sure you're in Degrees mode!):

`m\angle B\approx 80.27^\circ`

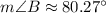
The interior angles of a triangle must total 180°. Hence:

`m\angle A+m\angle B+m\angle C=180^\circ`

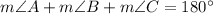
Substitute in known values:

`(40^\circ)+(80.27^\circ)+m\angle C=180^\circ`

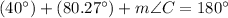
Therefore:

`m\angle C\approx 59.73^\circ`

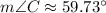
Lastly, to find AB or c, we can use the Law of Cosines:

`c^2=a^2+b^2-2ab\cos(C)`

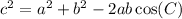
a = 15, b = 23, and to prevent rounding errors, we will use the exact value for C. Recall that we know that:

`m\angle A+m\angle B+m\angle C=180^\circ`

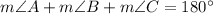
Using the exact value for ∠B, we acquire:

`40^\circ+\displaystyle \sin^(-1)(23\sin40^\circ)/(15)+m\angle C=180^\circ`

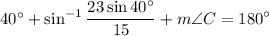
Therefore:

`\displaystyle m\angle C=\left(140-\sin^(-1)(23\sin40)/(15)\right)^\circ`

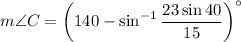
Substitute:

`\displaystyle c^2=(15)^2+(23)^2-2(15)(23)\cos\left(140-\sin^(-1)(23\sin40^\circ)/(15)\right)`

Simplify and take the square root of both sides.

`\displaystyle c=\sqrt{754-690\cos\left(140-\sin^(-1)(23\sin40^\circ)/(15)\right)}`

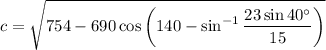
And use a calculator:

`c\approx 20.15`

Answer 2

Hi! The person above is actually correct, just that it needed to be rounded to the nearest tenth. Check the picture for confirmation. Hope this helped <3

Explanation:

The measure of angle B is approximately

80.3

The measure of angle C is approximately

59.7

The length of side AB is approximately

20.2

I got it correct on Edmentum/Plato