Question

I dont know how to do this

Answer 1

`\textsf{D.} \quad \left[\left(2+k\cdot(3)/(n)\right)^2+9\right] \left((3)/(n)\right)`

Explanation:

The Riemann sum is an approximation of the area under a curve using a series of rectangles.

A right Riemann sum uses rectangles where the curve of the function f(x) passes through the top-right vertices of the rectangles.

Definite Integral Notation (right Riemann Sum)

The area under the curve of f(x) on the interval [a, b] is represented by:

`\boxed{\begin{array}{l}\displaystyle \int^b_af(x)\; \text{d}x=\lim_(n \to \infty)\sum^n_(k=1)f(x_k) \cdot \Delta x\\\\\\\textsf{where $\Delta x=(b-a)/(n)$ and $x_k=a+\Delta x \cdot k$}\\\\\end{array}}`

where:

• Δx is the width of each rectangle.
• 
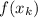  `f(x_k)` is the height of each rectangle.
• 
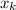  `x_k` is the right endpoint of each rectangle.
• n is the number of rectangles.

The given interval is [2, 5]. Therefore, a = 2 and b = 5.

As f(x) = x² + 9 then:

`f(x_k)=f(a+\Delta x k)=(a+\Delta x\cdot k)^2+9=\left(a+(b-a)/(n)\cdot k\right)^2+9`

Substitute a, b, and
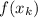`f(x_k)` into the summation formula:

`\displaystyle \lim_(n \to \infty)\sum^n_(k=1)\left(\left(a+(b-a)/(n)\cdot k\right)^2+9\right) \cdot (b-a)/(n)`

`\displaystyle \lim_(n \to \infty)\sum^n_(k=1)\left(\left(2+(5-2)/(n)\cdot k\right)^2+9\right) \cdot (5-2)/(n)`

`\displaystyle \lim_(n \to \infty)\sum^n_(k=1)\left(\left(2+(3)/(n)\cdot k\right)^2+9\right) \cdot (3)/(n)`

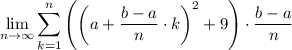
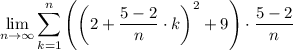
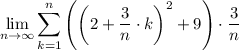
Therefore, the area (in square units) of the kth rectangle from the right is:

`\left[\left(2+k\cdot(3)/(n)\right)^2+9\right] \left((3)/(n)\right)`