Question

If Jackson deposits $50 at the end of each month in a savings account earning interest rate at a rate of 3%/ year compounded monthly. How much will he have on deposit in his savings account at the end of 4 years assuming makes no withdrawals during that period?(Round your answer to the nearest cont.)$

Answer 1

Jackson will have approximately $2,696.04 on deposit in his savings account at the end of 4 years, assuming he makes no withdrawals during that period.

To calculate the future value of Jackson's savings account after 4 years with monthly compounding interest, you can use the future value of an ordinary annuity formula:

`F V=P * ((1+r)^(n t)-1)/(r)`

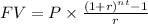
where:

FV is the future value of the annuity,

P is the monthly deposit (in this case, $50),

r is the monthly interest rate (in decimal form),

n is the number of compounding periods per year (in this case, 12 since it's compounded monthly),

t is the number of years.

In this scenario, P=50, r=0.03/12 (monthly interest rate), n=12, and t=4.

`F V=50 * (\left(1+(0.03)/(12)\right)^(12 * 4)-1)/((0.03)/(12))`

Now, calculate this expression to find the future value.

`\begin{aligned}& F V \approx 50 * ((1+0.0025)^(48)-1)/(0.0025) \\& F V \approx 50 * ((1.0025)^(48)-1)/(0.0025)\end{aligned}`

`\begin{aligned}& F V \approx 50 * (1.134802-1)/(0.0025) \\& F V \approx 50 * (0.134802)/(0.0025) \\& F V \approx 50 * 53.9208\end{aligned}`

`FV \approx \:\$2,696.04.`

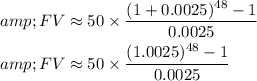
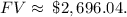
The correct result is approximately $2,696.04.