Question

A​ full-time worker aged 35 invests ​$750 a month in a fund which has an average yearly return of 6.0​% compounded monthly. (a) The worker wants to estimate what they will have for retirement when they are 60 years old if the rate stays constant. Assume monthly compounding. ​(b) If the worker makes no further deposits and makes no withdrawals after age 60​, how much will they have for retirement at age 65​?

(a) How much money will the worker have in their fund when they are 60 years​ old?
(b) If the worker makes no further deposits and makes no withdrawals after age 60​, how much will they have for retirement at age 65​?

Answer 1

The worker will have approximately $1,831.05 in their fund when they are 60 years old. They will have approximately $6,124.64 for retirement at age 65 if they make no further deposits and withdrawals.

Step-by-step explanation:

To find the amount of money the worker will have in their fund when they are 60 years old, we can use the formula for compound interest:

• P = A / (1+r/n)^(n*t)

where:

• P is the principal amount
• A is the final amount
• r is the interest rate (as a decimal)
• n is the number of times interest is compounded per year
• t is the number of years

In this case, the principal amount is $0 since the worker starts with $0 and makes monthly deposits, the interest rate is 0.06 (6% as a decimal), the number of times interest is compounded per year is 12 (since it is compounded monthly), and the number of years is 25 (60 - 35).

• P = 0 / (1+0.06/12)^(12*25)
• P = 0
• A = $750 * (1+0.06/12)^(12*25)
• A ≈ $750 * 2.44140625
• A ≈ $1,831.05

So, when the worker is 60 years old, they will have approximately $1,831.05 in their fund.

To find the amount of money the worker will have for retirement at age 65 if they make no further deposits and withdrawals, we can use the same formula for compound interest. However, instead of using 25 years, we will use 30 years since the worker will be retired for 5 years after age 60.

• P = $1,831.05
• A = $1,831.05 * (1+0.06/12)^(12*30)
• A ≈ $1,831.05 * 3.34597285
• A ≈ $6,124.64

Therefore, the worker will have approximately $6,124.64 for retirement at age 65 if they make no further deposits and withdrawals.

Answer 2

To calculate the amount of money the worker will have at age 60, use the formula for compound interest. The worker will have approximately $493,373.16. To calculate the amount of money the worker will have at age 65, use the same formula with a time period of 30 years. The worker will have approximately $805,738.84.

Step-by-step explanation:

In order to calculate the amount of money the worker will have in their fund when they are 60 years old, we need to use the formula for compound interest. We have the monthly deposit of $750, the annual interest rate of 6.0% compounded monthly, and the time period of 25 years (60 - 35). We can use the formula:

`A = P(1 + r/n)^(nt)`

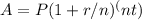
Where:
A = the future value of the investment
P = the principal investment amount (monthly deposit)
r = the annual interest rate (as a decimal)
n = the number of times that interest is compounded per year
t = the number of years

Plugging in the values, we get:

`A = 750(1 + 0.06/12)^(12) *^(25)`

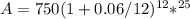
Using a calculator, we find that A ≈ $493,373.16.

To calculate the amount of money the worker will have for retirement at age 65, we can use the same formula, but with a time period of 30 years (65 - 35). Plugging in the values, we get:

A = 750(1 + 0.06/12)⁽¹²ˣ²⁵⁾

Using a calculator, we find that A ≈ $805,738.84.