Question

$1,200 are deposited into an account with

a 6.75% interest rate, compounded
quarterly.
Find the accumulated amount after
20 years.
Hint: A = P(1+r/k)^kt

Answer 1

Answer: 4577.06

Work Shown:

A = P(1+r/k)^(kt)

A = 1200(1+0.0675/4)^(4*20)

A = 4577.06277131092

A = 4577.06

Answer 2

Accumulated amount =$4577.062771

Explanation:

Given:

• Principal(p) = $1,200
• Interest rate(r) = 6.75% per year = 0.0675

• Number of years (t) = 20 years

• Number of compounding periods per year (k) = 4

Formula:

The formula for compound interest is:

`\sf A = P\left(1 + (r)/(k)\right)^(kt)`

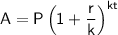
where:

• A is the accumulated amount
• P is the principal
• r is the interest rate
• k is the number of compounding periods per year
• t is the number of years

Solution:

Substitute the given values, we get:

`\sf A = 1,200\left(1 + (0.0675)/(4)\right)^(4* 20)`

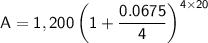
Evaluating the expression in the calculator, we get:

`\sf A = 1,200\left(1 + 0.016875\right)^(80)`

`\sf A = 1,200\left(1.016875\right)^(80)`

`\sf \sf A = 1,200*3.814218976`

`\sf A = 4577.062771`

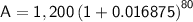
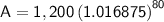
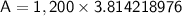
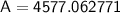
Therefore, the accumulated amount after 20 years is $4577.062771.