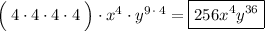Question

Simplify. Write the answer using positive exponents only. (4xy^(9))^(4)

Answer 1

`256x^4y^(36)`

Explanation:

We can simplify the expression:

`\left(\frac{}{}4xy^9\,\right)^4`

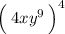
using the power of a product rule, which states that:

`(A \cdot B)^C = A^C \cdot B^C`

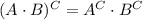
First, we can rewrite the value inside the parentheses as a product of three factors.

`\left(\frac{}{}4xy^9\,\right)^4 = \left(\frac{}{}4 \cdot x \cdot y^9\,\right)^4`

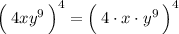
Then, we can use the above power of a product rule to simplify.

`\left(\frac{}{}4 \cdot x \cdot y^9\,\right)^4 = 4^4 \cdot x^4 \cdot (y^9)^4`

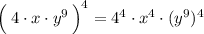
Next, we can simplify the first factor (
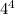`4^4`) using the definition of an exponent and the third factor using the exponent product rule, which states that:

`(A^B)^C = A^(B\,\cdot\, C)`

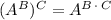
Hence the expression becomes:

`4^4 \cdot x^4 \cdot (y^9)^4 = \left(\frac{}{}4 \cdot 4 \cdot 4 \cdot 4\frac{}{}\right) \cdot x^4 \cdot y^{9 \, \cdot \, 4`

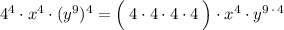
Finally, we can fully simplify the expression by executing every instance of multiplication of constants.

`\left(\frac{}{}4 \cdot 4 \cdot 4 \cdot 4\frac{}{}\right) \cdot x^4 \cdot y^(9 \, \cdot \, 4) = \boxed{256x^4y^(36)}`