Question

Select the correct expressions. Identify each expression and value that represents the area under the curve y= -0.01x^2+40 on the interval [-10,10] . (one in approximate form and one in exact form with the limit)

Answer 1

`\displaystyle \lim_(n \to \infty)\left[\sum^n_(k=1)\left\{-0.01\left(-10+(20k)/(n)\right)^2+40\right\} (20)/(n)\right]\; \sf square\;units`

`\displaystyle \lim_(n \to \infty)\left[\sum^n_(k=1)\left((780)/(n)+(80k)/(n^2)-(80k^2)/(n^3)\right)\right]\; \sf square\;units`

793.33 square units

Explanation:

Use the Riemann sum to approximate the area under a curve using a series of rectangles.

A right Riemann sum uses rectangles where the curve of the function f(x) passes through the top-right vertices of the rectangles.

Definite Integral Notation (right Riemann Sum)

The area under the curve of f(x) on the interval [a, b] is represented by:

`\boxed{\begin{minipage}{6cm}$\displaystyle \int^b_af(x)\; \text{d}x=\lim_(n \to \infty)\sum^n_(k=1)f(x_k) \cdot \Delta x$\\\\\\where $\Delta x=(b-a)/(n)$ and $x_k=a+\Delta x \cdot k&\\\end{minipage}}`

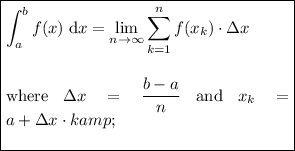
where:

• Δx is the width of each rectangle.
• 
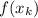  `f(x_k)` is the height of each rectangle.
• 
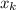  `x_k` is the right endpoint of each rectangle.
• n is the number of rectangles.

The given interval is [-10, 10]. Therefore, a = -10 and b = 10:

`\implies \Delta x=(b-a)/(n)=(10-(-10))/(n)=(20)/(n)`

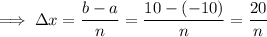
As f(x) = -0.01x² + 40 then:

`\implies f(x_k)=f(a+k \Delta x)=-0.01(a+k\Delta x)^2+40=-0.01\left(-10+(20k)/(n)\right)^2+40`

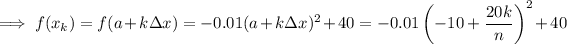
Substituting into the summation formula gives:

`\begin{aligned}\displaystyle \int^(10)_(-10) -0.01x^2+40\; \text{d}x&=\lim_(n \to \infty)\sum^n_(k=1)\left(-0.01\left(-10+(20k)/(n)\right)^2+40\right) \cdot \left((20)/(n)\right)\end{aligned}`

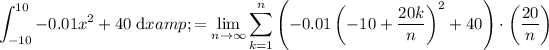
Expand the summation:

`\displaystyle \lim_(n \to \infty)\sum^n_(k=1)\left(-0.01\left(-10+(20k)/(n)\right)^2+40\right) \cdot \left((20)/(n)\right)`

`\displaystyle \lim_(n \to \infty)\sum^n_(k=1)\left(-0.01\left(100-(400k)/(n)+(400k^2)/(n^2)\right)+40\right) \cdot \left((20)/(n)\right)`

`\displaystyle \lim_(n \to \infty)\sum^n_(k=1)\left(-1+(4k)/(n)-(4k^2)/(n^2)+40\right) \cdot \left((20)/(n)\right)`

`\displaystyle \lim_(n \to \infty)\sum^n_(k=1)\left(-(20)/(n)+(80k)/(n^2)-(80k^2)/(n^3)+(800)/(n)\right)`

`\displaystyle \lim_(n \to \infty)\sum^n_(k=1)\left((780)/(n)+(80k)/(n^2)-(80k^2)/(n^3)\right)`

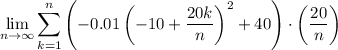
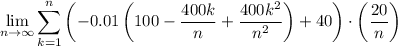
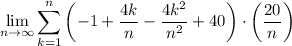
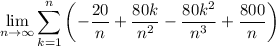
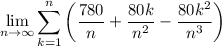
Therefore, the approximations of the area under the curve are:

`\displaystyle \lim_(n \to \infty)\left[\sum^n_(k=1)\left\{-0.01\left(-10+(20k)/(n)\right)^2+40\right\} (20)/(n)\right]\; \sf square\;units`

`\displaystyle \lim_(n \to \infty)\left[\sum^n_(k=1)\left((780)/(n)+(80k)/(n^2)-(80k^2)/(n^3)\right)\right]\; \sf square\;units`

`\hrulefill`

To find the exact area under the given curve, use the second part of the Fundamental Theorem of Calculus:

`\boxed{\begin{array}{l}\textsf{If}\;\displaystyle \int \text{f}(x)\;\text{d}x=\text{g}(x)+\text{C}\; \textsf{then:}\\\\\displaystyle \int^b_a \text{f}(x)\; \text{d}x=\left[\text{g}(x)\right]^b_a=\text{g}(b)-\text{g}(a)\\\\\textsf{where}\;a\;\textsf{is the lower limit and}\;b\;\textsf{is the upper limit.}\\\end{array}}`

Therefore:

`\displaystyle \int^(10)_(-10) \left(-0.01x^2+40\right)\:\:\text{d}x`

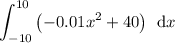
Evaluate the integral by using the following integral rules:

`\boxed{\begin{minipage}{4 cm}\underline{Integrating $x^n$}\\\\$\displaystyle \int x^n\:\text{d}x=(x^(n+1))/(n+1)\;(+\;\text{C})$\end{minipage}}`

`\boxed{\begin{minipage}{5.1 cm}\underline{Integrating a constant}\\\\$\displaystyle \int n\:\text{d}x=nx\;(+\;\text{C})$\\\\(where $n$ is any constant value) \end{minipage}}`

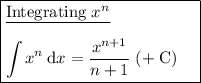
Therefore:

`\begin{aligned}\displaystyle \int^(10)_(-10) \left(-0.01x^2+40\right)\:\:\text{d}x&=\left[(-0.01x^(2+1))/(2+1)+40x\right]^(10)_(-10)\\\\&=\left[-(x^(3))/(300)+40x\right]^(10)_(-10)\\\\&=\left(-((10)^(3))/(300)+40(10)\right)-\left(-((-10)^(3))/(300)+40(-10)\right)\\\\&=\left(-(10)/(3)+400\right)-\left((10)/(3)-400\right)\\\\&=-(20)/(3)+800\\\\&=(2380)/(3)\\\\&=793.33\; \sf (2\;d.p.)\end{aligned}`

Therefore, the exact area under the given curve on the interval [-10, 10] is 793.33 square units (2 d.p.).