Question

Does the point (5,10) satisfy the equation: 4y-2x=20

Answer 1

• Answer:

`\Large{\boxed{\sf The \ point \ \underline{does \ not} \ satisfy \ the \ equation.}}`

`\\`

• Explanation:

When we say that a point satisfies a linear equation, we mean that if we substitute its x-coordinate (also known as its abscissa) for x and its y-coordinate (also known as its ordinate) for y, the equality is verified.

`\\`

Let's identify the values of x and y:

`(\underbrace{\sf 5}_(\sf x) \ , \ \overbrace{\sf 10}^(\sf y))`

`\\`

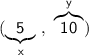
Substituting our values in the left side of the equation, we get:

`\sf 4y - 2x = 4\ast10 - 2\ast 5 = 40 - 10 = \boxed{\boxed{\sf 30 \\eq 20}}`

`\\ \\`

∴ The point does not satisfy the equation.