Question

An a.c. source of 200 V, 50 Hz is connected across a 300 ohm resistor and a capacitor of 25/π µF in series.

Calculate:
(a) the reactance,
(b) impedance and
(c) current in the circuit.​

Answer 1

Let's embark on an electrifying adventure through this circuit puzzle!

So, we've got this lively AC source, buzzing with 200 volts and pulsating at 50 Hz. It's connected to a 300-ohm resistor, walking hand-in-hand with a capacitor of 25/π microfarads in a series arrangement.

(a) Reactance, think of it like the "AC resistance" of the capacitor. We'll unravel this value using a cool formula that considers frequency and capacitance. It tells us how the capacitor responds to the dance of the AC signal.

(b) Impedance! It's the combined resistance and reactance that the circuit throws at the flowing current. For this series of resistor and capacitor, we'll blend both resistance and reactance to find the total hindrance in the circuit's path.

(c) Last but not least, let's uncover the current flowing through this circuit. We'll tap into Ohm's Law, using the circuit's voltage and impedance to reveal this crucial flow.

Shall we kick things off by discovering the reactance of the capacitor? Once we've got that, the journey to determine impedance and current in our electric wonderland will be smooth sailing!

Step-by-step explanation:

<3

Answer 2

a) Reactance (Xc) of the capacitor = 400 ohms

b) Impedance (Z) of the circuit = 500 ohms

c) Current (I) in the circuit = 0.4 A

Step-by-step explanation:

Given values:

• A.C. source voltage (V) = 200 V
• Frequency (f) = 50 Hz
• Resistor (R) = 300 ohms
• Capacitance (C) = 25/π µF

Calculations for the reactance, impedance, and current in the circuit:

(a) Reactance is opposition to the flow of alternating current by a capacitor or inductor.

The reactance of the capacitor is given by:

`\boxed{\boxed{\sf X_c =( 1 )/(2\pi fC)}}`

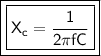
where:

• f is the frequency of the source (50 Hz)
• C is the capacitance of the capacitor (25/π µF)
• Xc is the reactance.

Plugging in the values, we get:

`\sf X_c =(1)/( (2\pi * 50 Hz * (25)/(\pi) * 10^(-6)\: F))`

`\sf X_c =(\pi * 10^6)/( (2\pi* 50* 25))`

`\sf X_c =( 10^6)/( 2500)`

`\sf X_c =400 \textsf{ ohms}`

`\dotfill`

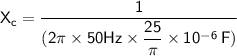
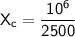
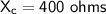
(b) Impedance is total opposition to the flow of alternating current in a circuit.

The impedance of the circuit is given by:

`\boxed{\boxed{ \sf Z = √((R^2 + Xc^2)}}`

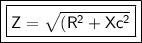
where:

• Z is impedance.
• R is resistor. (300 ohms)
• Xc is the reactance. (400 ohms)

Plugging in the values, we get:

`\sf Z = √(300^2 + 400^2)`

`\sf Z = 500\textsf{ ohms }`

`\dotfill`

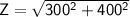
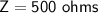
(c) Current is flow of electric charge through a circuit.

The current in the circuit is given by:

`\boxed{\boxed{\sf I = (V )/( Z)}}`

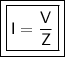
where:

• I is current.
• V is voltage. (200 V)
• Z is impedance. (500 V)

Plugging in the values, we get:

`\sf I = \frac{200 V }{ 500 \textsf{ ohms}}`

`\sf I = 0.4 \textsf{ amps}`

`\dotfill`

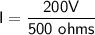
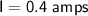
Summary:

a) Reactance (Xc) of the capacitor = 400 ohms

b) Impedance (Z) of the circuit = 500 ohms

c) Current (I) in the circuit = 0.4 A