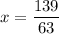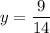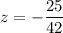Question

Can you please solve this system of equations by turning them into an Augmented matrix?

Answer 1

`\textsf{M}=\left[\begin{array}r-3&0&4&-9\\0&1&-9&6\\0&5&-3&5\end{array}\right]`

`x=(139)/(63), \quad y=(9)/(14), \quad z=-(25)/(42)`

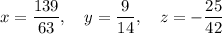
Explanation:

An augmented matrix is formed by combining the matrices with the coefficient terms and the constant terms of a system of linear equations.

System of three linear equations:

`a_1x + b_1y + c_1z = d_1`

`a_2x + b_2y + c_2z = d_2`

`a_3x + b_3y + c_3z = d_3`

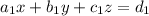
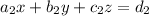
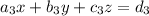
The matrix of coefficients (A) of the three linear equations is:

`\textsf{A}=\left[\begin{array}{ccc}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{array}\right]`

The matrix of constant terms (B) of the three linear equations is:

`\textsf{B}=\left[\begin{array}{c}d_1\\d_2\\d_3\end{array}\right]`

The augmented matrix (M) is the combination of the matrices with the coefficient terms and the constant terms:

`\textsf{M} = \left[\begin{array}c\sf A & \sf B\end{array}\right]`

`\textsf{M}=\left[\begin{array}ccca_1&b_1&c_1&d_1\\a_2&b_2&c_2&d_2\\a_3&b_3&c_3&d_3\end{array}\right]`

`\hrulefill`

The given system of equations is:

`\begin{aligned}-3x &= -9 - 4z\\y &= 6 + 9z\\-3z &= -5y + 5\end{aligned}`

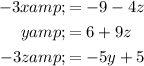
Rearrange each equation so that it is in ax + by + cz = d form:

`\begin{aligned}-3x&=-9-4z\\-3x+4z&=-9-4z+4z\\-3x+4z&=-9\\-3x+0y+4z&=-9\end{aligned}`

`\begin{aligned}y&=6+9z\\y-9z&=6+9z-9z\\y-9z&=6\\0x+y-9z&=6\end{aligned}`

`\begin{aligned}-3z&=-5y+5\\-3z+5y&=-5y+5+5y\\-3z+5y&=5\\0x+5y-3z&=5\end{aligned}`

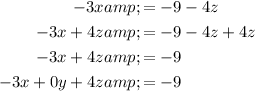
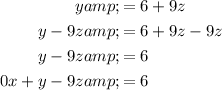
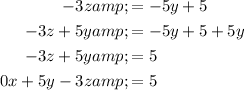
The matrix of coefficients (A) of the three linear equations is:

`\textsf{A}=\left[\begin{array}{rrr}-3&0&4\\0&1&-9\\0&5&-3\end{array}\right]`

The matrix of constant terms (B) of the three linear equations is:

`\textsf{B}=\left[\begin{array}{r}-9\\6\\5\end{array}\right]`

Therefore, the augmented matrix (M) is:

`\textsf{M}=\left[\begin{array}rrr-3&0&4&-9\\0&1&-9&6\\0&5&-3&5\end{array}\right]`

Each row corresponds to an equation in the system, and the last column contains the constants from the right-hand side of each equation. The columns before the vertical bar represent the coefficients of the variables x, y, and z in the respective equations.

To solve the augmented matrix, use elementary row operations to convert it into the identity matrix

`\left[\begin{array}c1&0&0&p\\0&1&0&q\\0&0&1&r\end{array}\right]`

where the solution to the system will be x = p, y = q, and z = r.

Elementary row operations are:

• Interchange two rows.
• Multiply a row by a constant.
• Add a multiple of a row to another row.

`\textsf{M}=\left[\begin{array}r-3&0&4&-9\\0&1&-9&6\\0&5&-3&5\end{array}\right]`

The first step is to get a 1 in the upper left hand corner. To do this, multiply row 1 (R₁) by -1/3:

`\left[\begin{array}r-3&0&4&-9\\0&1&-9&6\\0&5&-3&5\end{array}\right]\begin{array}{c}-(1)/(3)R_1\\\rightarrow\end{array}\left[\begin{array}rrr1&0&-(4)/(3)&3\\0&1&-9&6\\0&5&-3&5\end{array}\right]`

The next step is to turn the 5 of row 3 (R₃) into a zero. To do this, subtract 5R₂ from R₃:

`\left[\begin{array}rrr1&0&-(4)/(3)&3\\0&1&-9&6\\0&5&-3&5\end{array}\right]\begin{array}{c}R_3-5R_2\\\rightarrow\end{array}\left[\begin{array}rrr1&0&-(4)/(3)&3\\0&1&-9&6\\0&0&42&-25\end{array}\right]`

Now multiply R₃ by 1/42 to turn 42 in R₃ into 1:

`\left[\begin{array}r1&0&-(4)/(3)&3\\0&1&-9&6\\0&0&42&-25\end{array}\right]\begin{array}{c}(1)/(42)R_3\\\rightarrow\end{array}\left[\begin{array}rrr1&0&-(4)/(3)&3\\0&1&-9&6\\0&0&1&-(25)/(42)\end{array}\right]`

Multiply R₃ by 4/3 and add this to R₁ to turn the -4/3 of R₁ into zero:

`\left[\begin{array}rrr1&0&-(4)/(3)&3\\0&1&-9&6\\0&0&1&-(25)/(42)\end{array}\right]\begin{array}{c}R_1+(4)/(3)R_3\\\rightarrow\end{array}\left[\begin{array}r1&0&0&(139)/(63)\\0&1&-9&6\\0&0&1&-(25)/(42)\end{array}\right]`

Multiply R₃ by 9 and add this to R₂ to turn the -9 of R₂ to zero:

`\left[\begin{array}r\vphantom{\frac12}1&0&0&(139)/(63)\\\vphantom{\frac12}0&1&-9&6\\\vphantom{\frac12}0&0&1&-(25)/(42)\end{array}\right]\begin{array}{c}R_2+9R_3\\\rightarrow\end{array}\left[\begin{array}rrr\vphantom{\frac12}1&0&0&(139)/(63)\\\vphantom{\frac12}0&1&0&(9)/(14)\\\vphantom{\frac12}0&0&1&-(25)/(42)\end{array}\right]`

Finally, read off the solutions for x, y and z from the rightmost column:

`x=(139)/(63)`

`y=(9)/(14)`

`z=-(25)/(42)`