Question

I need help urgently

Answer 1

(a) A = 0.0024 m²

(b) t = 0.131 s

Step-by-step explanation:
`\hrulefill`

(a) Finding Loop Area (A):
`\hrulefill`

In this part of the question, you're given the following information:

• Generator voltage (emf): 5.75 V
• Angular velocity: ω = 24.0 rad/s
• Magnetic field magnitude: B = 0.800 T
• Number of turns in the loop: N = 125

The induced emf in a coil in a generator is given as:

`\rightarrow \epsilon = NAB \omega`

Where:

• emf is the electromotive force (voltage) induced in the loop.
• N is the number of turns in the loop.
• A is the area of the loop.
• B is the magnetic field magnitude.
• ω is the angular velocity.

You are asked to find the loop area A. Rearranging the formula:

`\Longrightarrow \epsilon = NAB \omega\\\\\\\\\therefore A = (\epsilon)/(NB \omega)`

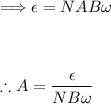
Now, substitute the given values:

`\Longrightarrow A = (5.75 \ V)/((125)(0.800 \ T)(24.0 \ (rad)/(s) ))\\\\\\\\\therefore \boxed{\boxed{A=0.0024 \ m^2 }}`

Thus, the area of the loop is found.

`\hrulefill`

(b) Finding Time Interval between Max and Min emf:
`\hrulefill`

In this part, you are asked to find the time interval between the maximum emf (+5.75 V) and the minimum emf (-5.75 V). The emf generated in a loop is sinusoidal in nature due to the rotation of the wheel.

To find the time interval between the maximum and minimum emf, you need to determine the time it takes for the emf to go from the maximum value to the minimum value within one cycle of the sinusoidal waveform. This time interval corresponds to half a period of the sinusoidal function.

The time period (T) of a sinusoidal function can be related to angular velocity ω by the formula:

`\rightarrow T = (2\pi)/(\omega)`

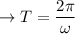
Plug in ω = 24 rad/s:

`\Longrightarrow T = (2\pi)/(24 \ (rad)/(s) )\\\\\\\\\Longrightarrow T = (\pi)/(12) \ s\\ \\\\\\\therefore T \approx 0.262 \ s`

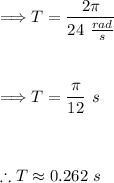
The time interval between the maximum and minimum emf is then half of the time period:

`\rightarrow \text{Time interval} \ (t) = (T)/(2) =(\pi)/(\omega)`

Substitute the given value of T to find the time interval in seconds:

`\Longrightarrow t = (0.262 \ s)/(2) \\\\\\\\\therefore \boxed{\boxed{ t=0.131 \ s }}`

Thus, the time interval is found.