Question

I plugged the equation into a calculator and I keep on getting the same “All real numbers”

Answer 1

Answer: Choice C.
`\text{x} \\e -1`

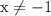
Reason:

The denominator
`\text{x}^2-6\text{x}-7` factors to
`(\text{x}-7)(\text{x}+1)`

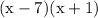
If x = 7 or x = -1, then the original denominator turns to 0. We cannot have 0 in the denominator. It leads to a division by zero error.

Therefore, we must exclude those x values from the domain.

The domain is the set of any real number but
`\text{x} \\e 7 \text{ and } \text{x} \\e -1`

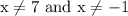
The
`\text{x} \\e 7` portion is already taken care of by the simplified expression. Note how we cannot plug x = 7 into this simplified expression because it makes the denominator zero. But we can plug x = -1 into the simplified version. We must exclude -1 from the domain however to ensure the domains line up perfectly.

The graph is shown below. We have a vertical asymptote at x = 7 and an open hole at x = -1.