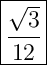Question

Find the ratio of the numerical value of the area, in square units, of an equilateral triangle of side length $1$ units to the numerical value of its perimeter, in units. Express your answer as a common fraction in simplest radical form.

Answer 1

`(√(3))/(12)`

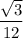
Explanation:

The formula for the area of an equilateral triangle is:

`\large\boxed{A=(√(3))/(4)s^2}`

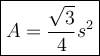
where "s" is the side length.

To calculate the area of an equilateral triangle with side length 1 unit, substitute s = 1 into the formula for area:

`A=(√(3))/(4) \cdot 1^2`

`A=(√(3))/(4) \cdot 1`

`A=(√(3))/(4) \; \sf square\;units`

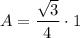
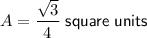
Therefore, the area of an equilateral triangle with side length 1 unit is:

`\boxed{\textsf{Area}=(√(3))/(4) \; \sf square\;units}`

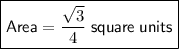
The perimeter of a two-dimensional shape is the distance all the way around the outside. Therefore, the perimeter of an equilateral triangle with side length 1 unit is 3 units (since an equilateral triangle has three sides of equal length).

`\boxed{\textsf{Perimeter}=3\; \sf units}`

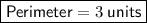
Therefore the ratio of the numerical value of the area to the numerical value of its perimeter is:

`\textsf{Area : Perimeter}=(√(3))/(4):3`

Express the ratio as a fraction:

`((√(3))/(4))/(3)=(√(3))/(4)\cdot (1)/(3)=(√(3))/(12)`

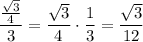
Therefore, the ratio of the numerical value of the area, in square units, of an equilateral triangle of side length 1 units to the numerical value of its perimeter, in units, expressed as a common fraction in simplest radical form is:

`\Large\boxed{(√(3))/(12)}`