Question

Let the vertices of a triangle are A(-3,2), B(5,8)and C(5,2) .If M₁, M₂ and M3 are the mid points of the line segments AB, BC and CA respectively of a triangle, find the co-ordinates of M₁, M₂ and M3.Also determine the type of the triangle M₁ M₂ M3.

please help me​

Answer 1

M₁ = (1, 5)

M₂ = (5, 5)

M₃ = (1, 2)

Right triangle

Explanation:

Given vertices of triangle ABC:

• A(-3, 2)
• B(5, 8)
• C(5, 2)

Given M₁, M₂ and M₃ are the midpoints of the line segments AB, BC and CA respectively, we can find the co-ordinates of M₁, M₂ and M₃ by using the midpoint formula.

`\boxed{\begin{minipage}{7.4 cm}\underline{Midpoint between two points}\\\\Midpoint $=\left((x_2+x_1)/(2),(y_2+y_1)/(2)\right)$\\\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the endpoints.\\\end{minipage}}`

M₁ is the midpoint of AB. Therefore:

`\begin{aligned}\sf M_1&=\left((x_B+x_A)/(2),(y_B+y_A)/(2)\right)\\\\&=\left((5+(-3))/(2),(8+2)/(2)\right)\\\\&=\left((2)/(2),(10)/(2)\right)\\\\&=\left(1,5\right)\\\\\end{aligned}`

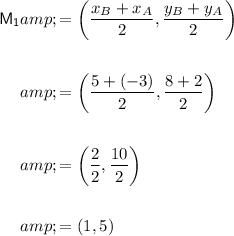
M₂ is the midpoint of BC. Therefore:

`\begin{aligned}\sf M_2&=\left((x_C+x_B)/(2),(y_C+y_B)/(2)\right)\\\\&=\left((5+5)/(2),(2+8)/(2)\right)\\\\&=\left((10)/(2),(10)/(2)\right)\\\\&=(5,5)\end{aligned}`

M₃ is the midpoint of CA. Therefore:

`\begin{aligned}\sf M_3&=\left((x_A+x_C)/(2),(y_A+y_C)/(2)\right)\\\\&=\left((-3+5)/(2),(2+2)/(2)\right)\\\\&=\left((2)/(2),(4)/(2)\right)\\\\&=(1,2)\end{aligned}`

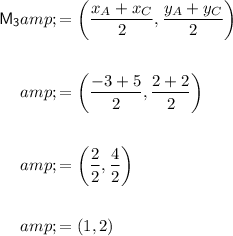
Therefore, the co-ordinates of midpoints M₁, M₂ and M₃ are:

• M₁ = (1, 5)
• M₂ = (5, 5)
• M₃ = (1, 2)

As M₁ and M₃ share the same x-coordinate, and M₁ and M₂ share the same y-coordinate, the type of triangle formed by the midpoints is a right triangle.