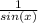Question

I need answers as well as their explanations.... i'd be delighted if anyone could help me....

Answer 1

Hope the picture will help you

Answer 2

Q 141. = b

Q 142 = b

Q 143 = c

Explanation:

* throughout these equations i have replaced theta with x so instead of cos² Ф it says cos²(x)

Q 141

this one is actually a trigonometry law that says cos²(x) + sin²(x) = 1

so the answer is simply 1 (b)

Q 142

for this question, it is easiest to break down sec² and tan² into their fractions which are also trigonometry laws:

sec² = 1 / cos²

tan² = sin² / cos²

so the question sec²(x) - tan²(x) can now be written:

`(1)/(cos^(2)(x) ) - (sin^(2) (x))/(cos^(2) (x))`

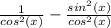
As the denominators are now the same, we can subtract the numerators. Using the same trigonometry we used for the first question ( sin² + cos² = 1) we can rearrange it into (1 - sin² = cos²) and use this to solve the subtraction of the numerators

`(1)/(cos^(2)(x) ) - (sin^(2) (x))/(cos^(2) (x)) = (cos^(2)(x) )/(cos^(2)(x) )`

`(cos^(2)(x))/(cos^(2)(x)) = 1`

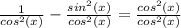
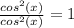
Q 143

same as the last question, we will split these into fractions using the trig laws.

sec(x) = 1 / cos(x)

cot(x) = 1 / tan(x)

tan(x) = sin(x) / cos(x)

So the equation now reads:

sec(x) × cot(x) =
`(1)/(cos(x))` ×
`(1)/(tan(x))`

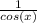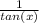
i will now convert tan(x) as shown above

`(1)/(cos(x))` ×
`(1)/((sin(x))/(cos(x)) )` =
`(1)/(cos(x))` ×
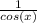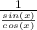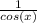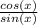`(cos(x))/(sin(x))` (let me know if you need an explanation of this step)

using fraction laws, you can cross out diagonal identical expressions (cos(x)), leaving 1 / sin (x)

`(1)/(cos(x))` ×
`(cos(x))/(sin(x))` =
`(1)/(sin(x))`

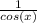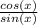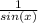
again let me know if you need an explanation of this step as i skipped a few steps due to assumed knowledge.

therefore the answer =
`(1)/(sin(x))`