Answer: 7 units right and 4 units up.
Explanation:
Parabolas are written in the vertex form of y = a(x - h)² + k where a is the amplitude, -h is the horizontal shift, and k is the vertical shift. From the given equation, we see that we have a shift of 7 units right and a shift of 4 units up.
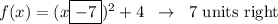

I have also attached a graph of both of these functions below, see attached.