Question

Portia is a designer working on creating plans for the city of Geocove's new waterpark. The graph shows her plan for a waterslide for young children. The equation that represents this line is y = -1/3x + 4. The x-axis represents the ground, and the y-axis represents one of the poles that will support the slide.

Each unit on each axis represents 1 foot. Suppose that a rider coming down this slide has a horizontal change of 6 feet. What is the value of their vertical change? Explain.

Answer 1

`y=\stackrel{\stackrel{m}{\downarrow }}{-\cfrac{1}{3}}x+4\qquad \impliedby \qquad \begin{array}c \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array} \\\\[-0.35em] ~\dotfill`

`slope=\cfrac{\stackrel{\textit{vertical change}}{Rise}}{\underset{\textit{horizontal change}}{Run}}\hspace{5em} slope=\cfrac{\stackrel{\textit{vertical change}}{1}}{\underset{\textit{horizontal change}}{3}} \\\\\\ \stackrel{ \textit{when the Run = 6, what's the Rise?} }{\stackrel{slope}{\cfrac{1}{3}}=\cfrac{\stackrel{\textit{vertical change}}{v}}{\underset{\textit{horizontal change}}{6}}}\implies \cfrac{1}{3}=\cfrac{v}{6}\implies \cfrac{6}{3}=v\implies \boxed{2=v}`

in this case the slope is -1/3, the negative part simply means the slope is going down from left-to-right, as it'd be the case in a waterslide.

Answer 2

Vertical change is 2 feet.

Explanation:

The equation of the line is
`\sf y = -(1)/(3)x + 4.`

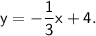
This equation can be rewritten as :
`\sf y -4 = -(1)/(3)x`

If a rider coming down this slide has a horizontal change of 6 feet, then their x-coordinate will change by 6.

This means that their new x-coordinate will be 6.

We can now plug this value of x into the equation for y to find their new y-coordinate.

`\sf \sf y -4 = -(1)/(3)* 6`

`\sf y - 4 = -2`

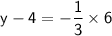
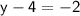
Adding 4 on both sides

`\sf y -4+4 =-2+4`

`\sf y = 2`

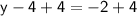
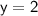
Therefore, the value of their vertical change is 2 feet.

In other words, if a rider starts at the point (0, 4) on the graph, and they move 6 units to the right, they will end up at the point (6, 2).

The vertical change is 4 - 2 = 2 feet.