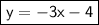Question

Write the equation of the line in fully simplified slope intercept form

Answer 1

y = 5x - 4

Explanation:

1st point (0,-4)

2nd point (-1,-1)

y2-y1/x2-x1

-1-4/-1-0= -5/-1 = 5

and slope is 4 because that is where the line intersects with the y axis.

Answer 2

Slope-intercept form is:
`\boxed{\sf y = -3x - 4}`

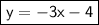
Explanation:

The slope-intercept form of a line is
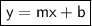`\boxed{\sf y = mx + b}`, where,

• m is the slope of the line
• b is the y-intercept.

In order to find the equation of line in fully simplified slope intercept form.

Let's take two points first:

`\sf (0,-4) \textsf{ and } (-4,8)`

To find the slope of the line, we can use the following formula:

`\sf m =( (y_2 - y_1) )/((x_2 - x_1))`

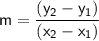
where
`\sf (x_1, y_1) \textsf{ and }(x_2, y_2)` are two points on the line.

In this case, we have the points (0, -4) and (-4, 8).

So, the slope is:

`\sf m =( (8 - (-4)) )/( (-4 - 0)) = (12 )/(-4 )= -3`

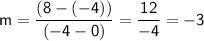
The y-intercept is the value of y when x is 0.

`\sf -4 = -3* 0 + b`

`\sf b = -4`

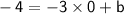
In this case, the y-intercept of y is -4.

Substituting value of m and b in slope intercept form, we get

`\sf y = -3x - 4`

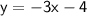
So, the equation of the line in slope-intercept form is:

`\boxed{\sf y = -3x - 4}`