Answer:
w = 28, 4 and l = 4, 28.
Explanation:
The formula for the area of a rectangle is
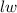 where l is the length and w is the width. Since the area of the rectangle is 112,
where l is the length and w is the width. Since the area of the rectangle is 112,
 . The formula for the perimeter of a rectangle is
. The formula for the perimeter of a rectangle is
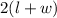 (simplified from
(simplified from
 ). The perimeter is 64, therefore
). The perimeter is 64, therefore
 . You can simplify the equation by dividing both sides by 2, giving you
. You can simplify the equation by dividing both sides by 2, giving you
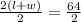 =
=
 .
.
Now you have a system of equations:
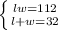 . The second equation gives you
. The second equation gives you
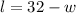 by subtracting w from both sides.
by subtracting w from both sides.
You can then plug in the expression for l into the first equation, getting
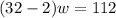 . Using the distributive property, you can simply the equation to get
. Using the distributive property, you can simply the equation to get
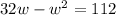 . By subtracting 112 on both sides, you get
. By subtracting 112 on both sides, you get
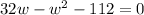 , or
, or
 by switching the places of
by switching the places of
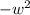 and 32w.
and 32w.
Then we can factor the equation. The only possible combination you can use to get
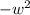 is -w multiplied by w. So, we have part of the new equation: (-w )(w ) = 0. Then, we need a pair of numbers that has a sum of 32 and a product of -112. You can list out all the factors of 112: 1, 2, 4, 7, 8, 14, 16, 28, 56, and 112. To get -112, you can just pick a pair that has a product of 112, but make one of the numbers negative.
is -w multiplied by w. So, we have part of the new equation: (-w )(w ) = 0. Then, we need a pair of numbers that has a sum of 32 and a product of -112. You can list out all the factors of 112: 1, 2, 4, 7, 8, 14, 16, 28, 56, and 112. To get -112, you can just pick a pair that has a product of 112, but make one of the numbers negative.
After some trial and error, we find that the pair we are looking for is 28 and -4. We are done factoring the equation to get
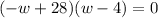 . We don't put -4 in the first set of parentheses because the product of a negative number and another negative number is a positive number. Knowing that 28 is smaller than 32, we can multiply the -w with the -4 to get a positive 4w. Adding that to the 28w we have from the product of 28 and w, we get the 32w we're looking for.
. We don't put -4 in the first set of parentheses because the product of a negative number and another negative number is a positive number. Knowing that 28 is smaller than 32, we can multiply the -w with the -4 to get a positive 4w. Adding that to the 28w we have from the product of 28 and w, we get the 32w we're looking for.
Now we know that
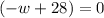 and
and
 For the first equation, we subtract 28 on both sides to give us
For the first equation, we subtract 28 on both sides to give us
 . Dividing both sides by -1 gives us
. Dividing both sides by -1 gives us
 . However, the second equation gives us
. However, the second equation gives us
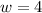 by adding 4 to both sides.
by adding 4 to both sides.
Therefore, w has two solutions: 28 and 4. Using
 , we can plug in w to get
, we can plug in w to get
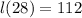 or
or
 . This also gives us two solutions for l: l = 4 or l = 28.
. This also gives us two solutions for l: l = 4 or l = 28.
We now have our final answers: w = 28, 4 and l = 4, 28.