Question

15. Sunil borrowed a certain sum from a bank at 5% per annum compound interest. He cleared the loan by paying Rs. 31,500 at the end of the first year and Rs. 22,050 at the end of the second year. a) Find the sum that he borrowed. b) How much more amount would he need if he cleared the loan only at the end of the second year?​

Answer 1

a) Rs. 50,000

b) Rs, 1,575

Explanation:

Part a

To find the total amount that Sunil borrowed, we can use the formula for compound interest.

`\boxed{\begin{minipage}{8.5 cm}\underline{Compound Interest Formula}\\\\$ A=P\left(1+(r)/(n)\right)^(nt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $n =$ number of times interest is applied per year \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}`

In this case, as the interest rate is 5% and it is applied annually, then:

• r = 5% = 0.05
• n = 1

Substituting these values of r and n into the compound interest formula gives:

`A=P\left(1+(0.05)/(1)\right)^(1 \cdot t)`

`A=P\left(1.05\right)^(t)`

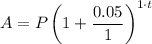
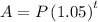
The balance of the loan (A) at the end of the first year is when t = 1. Therefore:

`A=P(1.05)^1`

`A=1.05P`

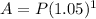
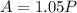
We are told that Sunil paid Rs. 31,500 at the end of the first year.

Therefore, the balance of the loan at the end of the first year after Sunil's payment is 1.05P less the amount he paid at that point:

`1.05P-31500`

To find the expression for the balance of the loan at the end of the second year, multiply the balance at the end of the first year by 1.05 (since 5% interest is applied each year).

Therefore, the balance of the loan at the end of the second year is given by:

`1.05(1.05P-31500)`

We are told that Sunil paid Rs. 22,050 at the end of the second year, and by paying this amount, Sunil cleared the loan. Therefore, we can subtract 22,050 from the balance of the loan at the end of the second year, and equate it to zero:

`1.05(1.05P-31500)-22050=0`

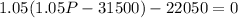
To find the sum Sunil borrowed, solve the equation for P:

`\begin{aligned}1.05(1.05P-31500)-22050&=0\\\\1.05(1.05P-31500)-22050+22050&=0+22050\\\\1.05(1.05P-31500)&=22050\\\\(1.05(1.05P-31500))/(1.05)&=(22050)/(1.05)\\\\1.05P-31500&=21000\\\\1.05P-31500+31500&=21000+31500\\\\1.05P&=52500\\\\(1.05P)/(1.05)&=(52500)/(1.05)\\\\P&=50000\end{aligned}`

Therefore, the sum that Sunil borrowed was Rs. 50,000.

`\hrulefill`

Part b

To find out how much Sunil paid in total by clearing the loan only at the end of the second year, substitute the found value of the sum he borrowed (P = Rs. 50,000) and t = 2 into the compound interest formula to calculate the balance of the loan after 2 years:

`A=50000(1.05)^2`

`A=50000(1.1025)`

`A=55125`

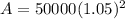
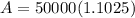
Therefore, the balance of the loan at the end of 2 years is Rs. 55,125.

So Sunil would have to pay a total of Rs. 55,125 to clear the loan only at the end of the second year.

To calculate how much more he would need to clear the loan only at the end of the second year, we can subtract the amounts he paid at the end of the first and second year (Rs. 31,500 and Rs. 22,050) from Rs. 55,125:

`55125-31500-22050=1575`
`55125-31500-22050=1\:\!575`

Therefore, Sunil would need to pay Rs, 1,575 more if he cleared the loan only at the end of the second year.

Answer 2

a. Sum: Rs. 50,000

b. needed more amount: Rs 1,575

Explanation:

For Question a.

In order to solve this problem, we can use the formula for compound interest:

`\boxed{\sf A = P(1 + r)^t}`

Where:

• A is the final amount after t years
• P is the principal amount (initial sum borrowed)
• r is the annual interest rate (as a decimal)
• t is the number of years

We are given that Sunil cleared the loan by paying Rs. 31,500 at the end of the first year and Rs. 22,050 at the end of the second year.

We can use this information to set up a system of equations:

Rate(r)= 5% = 0.05

time(t) = 1 year

After the first year:

• A = 31,500
• Rate(r)= 5% = 0.05
• time(t) = 1 year

Substituting value in formula, we get

`\sf P(1 + 0.05)^1 = 31,500`

`\sf P = (31500)/(1.05)`

P = Rs 30,000

The sum that he borrowed in first year is Rs 30,000

After the second year:

• A = 22,050
• Rate(r)= 5% = 0.05
• time(t) = 1 year

Substituting value in formula, we get

`\sf P(1 + 0.05)^2 = 22,050`

`\sf P (1.05)^2 = 22,050`

`\sf P*(1.1025) = 22,050`

`\sf P = (22,050)/(1.1025)`

P =Rs 20,000

Therefore, Sum he borrowed = Rs. 30000+ Rs. 20000=Rs. 50000

`\hrulefill`

For Question b.

We have,

• Sum = Rs 50,000
• Rate(r)= 5% = 0.05
• time(t) = 2 year

let's find interest amount for second year.

Substituting value in formula, we get

`\sf A = 50,000(1+ 0.05)^2`

`\sf A = 50,000*(1.05)^2`

`\sf A = 50,000*1.1025`

A = Rs 55,125

If Sunil cleared the loan only at the end of the second year, Sunil would need to pay : Rs. 55,125 - Rs. 31,500 - Rs. 22,050 = Rs. 1,575 more if he cleared the loan only at the end of the second year.