Question

Please help me to solve these problems.​

Answer 1

Answer:
a) Plot A: width = 10.93m (2d.p), length = 32.93m (2d.p)
Plot B: width = 15m, length = 24m
See calculations below...

b) No, they don't require equal lengths as they have different perimeters. See calculations below...

c) Plot B is more costly as it costs ₹97.27 more than A.

Explanation:

a) To find the length and breadths of both plots we have to use substitution and quadratics, so let's for now call the left field A and right field B.

To find the length and breadth of A:

`360=a(a+22)=a^2+22a\\a^2+22a-360=0\\`

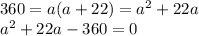
Now we use the quadratic formula (
`x=(-b\pm√(b^2-4ac))/(2a)$`)since we cannot factorise:

`a=(-22\pm√(22^2-4(1*-360)))/(2*1)$\\=-11+√(481)\;\;\;and\;\;-11-√(481)`

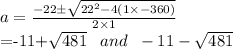
Since we cannot have negative length and breadth, our answer for a is
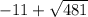`-11+√(481)` or 10.93 (2d.p.).

Therefore A: width = 10.93m (2d.p), length = 32.93m (2d.p)

Repeat to find the length and breadth of B:

`360=b(b+9)=b^2+9b\\b^2+9b-360=0\\`

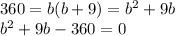
We can simply factorise this one to
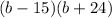`(b-15)(b+24)`, which gives us the solutions b = 15 and -24.

Again, since we can't have negative lengths, b = 15.

Therefore B: width = 15m, length = 24m

b) To figure this out we have use to see their perimeters so let's figure that out now we have their lengths and breadths.

To find A's perimeter:

`Perimeter\:A=2(2a+22) = 4a+44\\4(-11+√(481))+44 = 4√(481) = 82.73m\:(2d.p.)`

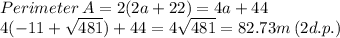
To find B's perimeter:

`Perimeter\;B=2(2b+9)=4b+18\\4(15)+18=78m`

Therefore the answer is no, they don't require equal lengths as they have different perimeters.

c) To find the cost of fencing, we times the cost (₹10 per meter) by the perimeter.

`Cost\:A=87.73\:(2d.p.)* 10=877.27 (2d.p.)\\Cost \:B = 78*10=780\\Difference=877.27-780=97.27`

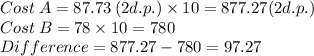
Plot B is more costly as it costs ₹97.27 more than A.

Hope this helps!!!