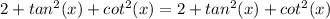Explanation:
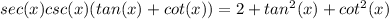
First, begin by simplifying the terms of each component listed in the problem:
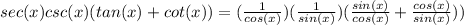
Then, begin by distributing
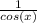 and
and
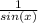 into the parentheses:
into the parentheses:
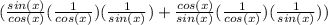
Next, cancel equivalent terms with one another:
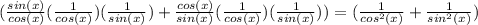
Further simplify each term:
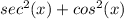
Using the Pythagorean Identities, allow
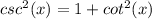 and
and
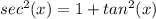 :
:

Simplify: