Question

I need help with part C! Thank you

Answer 1

Part A in Attachment.
`(x \approx -0.732, x \approx 1.302).`

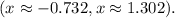
Part B: The right-end behavior model:
`(h(x) = \infty)`.

Part C: The limit:
`(\lim_{{x \to 8}} \frac{{f(x)}}{{h(x)}} = 0)`.

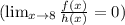Explanation:

Part A is featured in the Attachment.

B) To determine the right-end behavior model h(x) for f(x), we analyze the leading terms of the numerator and denominator of the function.

The leading term of the numerator is x^3, and the leading term of the denominator is x^2. Therefore, as x approaches positive infinity, the dominant term in the numerator becomes much larger than the term in the denominator. This implies that the function grows without bound as x increases.

Thus, the right-end behavior model h(x) for f(x) is:

`[ h(x) = \infty ]`

C) To determine
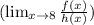`(\lim_{{x \to 8}} \frac{{f(x)}}{{h(x)}})` , we need to evaluate the limit of the function f(x) divided by the right-end behavior model h(x) as x approaches 8.

Since we don't have the specific expression for f(x), we cannot calculate the limit accurately without additional information. However, we can make an estimation based on the behavior of the function.

If the function f(x) approaches a finite value as x approaches 8, then the limit
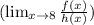`(\lim_{{x \to 8}} \frac{{f(x)}}{{h(x)}})` would be that finite value divided by (\infty), which would be zero.