Setting the lengths of the lines equal to each other, we have:
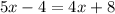
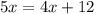 .
.
Isolating the x term, we get:
 .
.
Substituting
 back into the expressions for the lengths of the lines, we get:
back into the expressions for the lengths of the lines, we get:
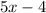
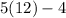

 ,
,
and
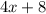
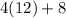
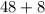
 .
.
So, the lengths of both lines are 56.
Note: We already know that both lines are congruent, so we don't need to substitute x=12 into both expressions.