Question

The scores of students on an exam are normally distributed with a mean of 211 and a standard deviation of 37. (a) What is the lower quartile score for this exam? Answer: (b) What is the upper quartile score for this exam? Answer:

Answer 1

The lower quartile score is approximately 184.25, and the upper quartile score is approximately 237.75.

To find the lower and upper quartile scores, we can use the z-score formula in combination with the properties of the standard normal distribution.

The lower quartile (Q1) corresponds to the 25th percentile, and the upper quartile (Q3) corresponds to the 75th percentile.

The z-score formula is given by:

`z=(X-\mu)/(\sigma)`

where:

X is the score,

μ is the mean,

σ is the standard deviation.

For the lower quartile (25th percentile), the z-score is approximately -0.6745.

For the upper quartile (75th percentile), the z-score is approximately 0.6745.

Now, we can use the z-score formula to find the corresponding scores.

(a) Lower Quartile Score
`\left(X_(Q 1)\right)`:

`z_(Q 1)=(X_(Q 1)-\mu)/(\sigma)`

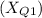Substitute the values:

`-0.6745=(X_(Q 1)-211)/(37)`

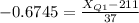
Solve for
`X_(Q 1)`:

`X_(Q 1)=-0.6745 * 37+211`

`X_(Q 1)=-0.6745 * 37+211 \approx 184.25`

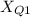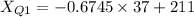
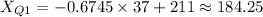
(b) Upper Quartile Score
`\left(X_(Q 3)\right):`

`z_(Q 3)=(X_(Q 3)-\mu)/(\sigma)`

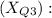
Substitute the values:

`0.6745=(X_(Q 3)-211)/(37)`

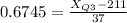
Solve for
`\left(X_(Q 3)\right):`

`X_(Q 3)=0.6745 * 37+211`

`X_(Q 3)=0.6745 * 37+211 \approx 237.75`

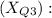
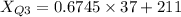
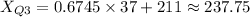
Question:

The scores of students on an exam are normally distributed with a mean of 211 and a standard deviation of 37.

(a) What is the lower quartile score for this exam? Answer:

(b) What is the upper quartile score for this exam? Answer: