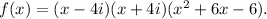Question

Given that-4i is a zero, factor the following polynomial function completely. Use the Conjugate Roots Theorem, if applicable. fQ) = x* + x3 + 10x + 16x - 96

Answer 1

To factor the given polynomial function completely, we use the Conjugate Roots Theorem. The factors of the polynomial are (x + 4i), (x - 4i), and (x - 6).

Step-by-step explanation:

To factor the given polynomial function completely, we first need to find its zeros. Since -4i is given as a zero, we know that its conjugate, 4i, must also be a zero. Therefore, the factors of the polynomial are (x + 4i) and (x - 4i). Now, we can divide the polynomial by these factors using polynomial long division or synthetic division to find the remaining factor. The resulting factor is (x - 6).

So, the completely factored form of the polynomial function is f(x) = (x + 4i)(x - 4i)(x - 6).

Answer 2

To factor the given polynomial function, use the Conjugate Roots Theorem and divide the polynomial by the factors obtained from the zeros. The fully factored form of the polynomial function is
`(x - 4i)(x + 4i)(x^2 + 6x - 6).`

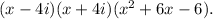
Step-by-step explanation:

To factor the polynomial function
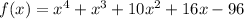`f(x) = x^4 + x^3 + 10x^2 + 16x - 96`, we start by using the Conjugate Roots Theorem.

Since -4i is a zero, we know that 4i is also a zero.

So the factors are (x + 4i) and (x - 4i). We can write them as (x - 4i)(x + 4i).

Next, we can divide the polynomial f(x) by (x - 4i)(x + 4i) to obtain the remaining factor.

Using long division or synthetic division, we find that the remaining factor is
`x^2 + 6x - 6.`

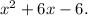
Therefore, the fully factored form of the polynomial function is
`f(x) = (x - 4i)(x + 4i)(x^2 + 6x - 6).`