Question

consider the following plot of residuals versus x for a regression analysis. which of the following statements is true about the regression model? select one: a. the residual plot shows a non-random pattern of residuals. b. a regression line on this residual plot could be used for prediction. c. a linear regression line is appropriate for this data. d. the residual plot shows a random pattern of residuals.

Answer 1

The residual plot shows a random pattern of residuals.

Step-by-step explanation:

The scatter plot of residuals versus x is used to determine whether a linear regression model is appropriate for the data.

If the residual plot shows a non-random pattern of residuals, it indicates that the linear regression model may not be appropriate for the data (option a).

A regression line on the residual plot is not used for prediction. It is used to assess the randomness of the residuals and to identify any patterns (option b).

If the residual plot shows a random pattern of residuals, it suggests that a linear regression line is appropriate for the data (option d).

Therefore, the correct statement is: The residual plot shows a random pattern of residuals (option d).

Answer 2

The correct answer is a. The residuals will have a sample mean of 1 which will be the center of the curved pattern demonstrated by the data points.

The correct statement indicating a property of a graph that is not indicative of a constant variance and an adequate fit for a linear model is:

a. The residuals will have a sample mean of 1 which will be the center of the curved pattern demonstrated by the data points.

Step-by-step explanation:

b. The graph should appear as a random scatter of points about zero on the residual's axis:

This statement is correct. A random scatter of points around zero suggests that the residuals have a constant variance.

c. The graph should indicate the same vertical spread for all values of
`\( \hat{y} \)`:

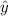This statement is correct. Homoscedasticity, or constant variance, is indicated when the spread of residuals is roughly the same across all levels of predicted values.

d. There should be no apparent patterns in the graph:

- This statement is correct. If there are no apparent patterns in the residual plot, it suggests that the linear model is adequate.

On the other hand, statement (a) is not correct because the residuals having a sample mean of 1 is not a typical property of a residual plot. The residuals should, on average, be centered around zero, not 1.

Complete the question:

A plot of the residuals versus the predicted values y^ can be used to check for a constant variance as well as to make sure that the linear model is adequate. Which of the following is not a property of a graph that indicates a constant variance and an adequate fit for a linear model?

a. The residuals will have a sample mean of 1 which will be the center of the curved pattern demonstrated by the data points.

b. The graph should appear as a random scatter of points about zero on the residual's axis.

c. The graph should indicate the same vertical spread for all values of y^.

d. There should be no apparent patterns in the graph.