Question

A survey found that 80% of college students believe that their online education courses are as good as or superior to courses that use traditional face-to-face instruction. a. Give the null hypothesis for testing the claim made by the survey. b. Give the rejection region for a two-tailed test conducted at a=0.10. a. What is the null hypothesis? Нор - 0.80 (Type an integer or a decimal.) b. What is the rejection region? Select the correct choice below and fill in any answer boxes to complete your choice. (Round to three decimal places as needed.) OA. Z< or z> OB. Zs OC. Z> OD <

Answer 1

The null hypothesis is that the proportion of college students believing that their online education courses are as good as or superior to face-to-face courses is equal to 80%. The rejection region for a two-tailed test conducted at a 0.10 significance level is z < -Zα/2 or z > Zα/2.

Step-by-step explanation:

The question can be answered as -

a. Null Hypothesis:

The null hypothesis for testing the claim made by the survey is that the proportion of college students believing that their online education courses are as good as or superior to face-to-face courses is equal to 80%. In symbolic form, H0: p = 0.80, where p represents the true proportion of college students with this belief.

b. Rejection Region:

The rejection region for a two-tailed test conducted at a 0.10 significance level is z < -Zα/2 or z > Zα/2. Since the significance level is 0.10, α/2 = 0.10/2 = 0.05. Looking up the z-value corresponding to a cumulative area of 0.05 in the standard normal distribution table, we find that Zα/2 = 1.645 (rounded to three decimal places).

Answer 2

1. a. The null hypothesis
`(\(H_0\))`for testing the claim is that the proportion of college students who believe online education is as good as or superior to traditional face-to-face instruction is equal to 80%, i.e., p = 0.80.

b. The rejection region for a two-tailed test conducted at
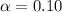`\( \alpha = 0.10 \)`is Z < -1.645 or Z > 1.645.

Step-by-step explanation:

a. The null hypothesis
`(\(H_0\))` is a statement of no effect or no difference. In this case, it is stated as p = 0.80, where p is the proportion of college students who believe online education is as good as or superior to traditional face-to-face instruction. This assumes that 80% is the baseline or expected proportion, and any deviation from this value will be considered in the alternative hypothesis.

b. The rejection region for a two-tailed test at
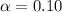`\( \alpha = 0.10 \)` involves finding critical values on both tails of the standard normal distribution. For a significance level of 0.10, the critical values are Z < -1.645 or Z > 1.645 . If the test statistic falls in either of these regions, the null hypothesis is rejected. This level of significance suggests a relatively high confidence level of 90% in a two-tailed test.

In summary, the null hypothesis is a statement of equality, assuming that 80% of college students find online education as good as or superior to traditional instruction. The rejection region in a two-tailed test at
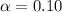`\( \alpha = 0.10 \)`is determined by critical values of Z , which areZ < -1.645 or Z > 1.645 . These critical values define the boundaries for rejecting the null hypothesis based on the level of significance.