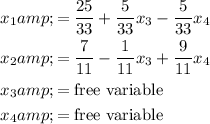Question

Solve the following equation for the matrix X : 1 0 0 0 1 1 0 1 2 Х 2 5 1 0 0 1 715 - 415 - 7/5 3/5 5 marks) Use the Gauss-Jordan method to solve the following system: X --3.21 + 2x2 - 13 +624 = -7 711 - 3.12 + 2x3 - 11:04 = 14 C1 - 24 = 1 (x, 82, 83, Xu) = /145, -1-25, 2-5,5) (3) 15 marks) 19 W 5 7 0 R Y 1 0 Р D F F G G H J K L Z V < B < N M. Z b command option

Answer 1

Problem 1: Matrix Equation

Given:

`$$\begin{pmatrix}1 & 0 & 0 \\0 & 1 & 1 \\0 & 1 & 2 \\\end{pmatrix} \(X\) \begin{pmatrix}2 & 1 \\3 & 4 \\\end{pmatrix} =\begin{pmatrix}2 & 5 \\1 & 0 \\0 & 1 \\\end{pmatrix}$$`

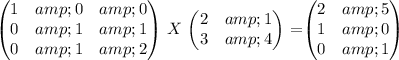
We need to find the matrix
`\(X\)` that satisfies the equation.

Let
`\(X\)` be the matrix:

`$$\begin{pmatrix}x_(11) & x_(12) \\x_(21) & x_(22) \\x_(31) & x_(32) \\\end{pmatrix}$$`

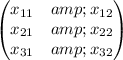
Performing the matrix multiplication:

`$$\begin{pmatrix}1 & 0 & 0 \\0 & 1 & 1 \\0 & 1 & 2 \\\end{pmatrix} *\begin{pmatrix}2 & 1 \\3 & 4 \\\end{pmatrix} =\begin{pmatrix}1 * 2 + 0 * 3 + 0 * 0 & 1 * 1 + 0 * 4 \\0 * 2 + 1 * 3 + 0 * 0 & 0 * 1 + 1 * 4 \\0 * 2 + 1 * 3 + 2 * 0 & 0 * 1 + 1 * 4 \\\end{pmatrix} =\begin{pmatrix}2 & 1 \\3 & 4 \\3 & 4 \\\end{pmatrix}$$`

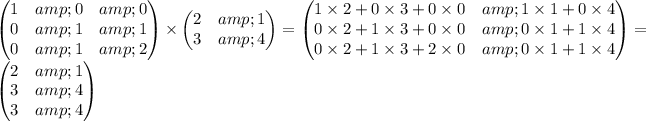
Comparing this with the given matrix:

`$$\begin{pmatrix}2 & 5 \\1 & 0 \\0 & 1 \\\end{pmatrix}$$`

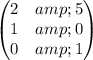
We can see that the matrices are not equal. Therefore, there is no matrix
`\(X\)` that satisfies the given equation.

Problem 2: System of Equations

Given the system of equations:

`$$\begin{align*}-3x_1 + 2x_2 - x_3 + 6x_4 &= -7 \\7x_1 - 3x_2 + 2x_3 - 11x_4 &= 14 \\x_1 - x_4 &= 1\end{align*}$$`

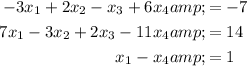
We can solve this system using the Gauss-Jordan method.

Writing the augmented matrix:

`$$\begin{bmatrix}-3 & 2 & -1 & 6 & -7 \\7 & -3 & 2 & -11 & 14 \\1 & 0 & 0 & -1 & 1 \\\end{bmatrix}$$`

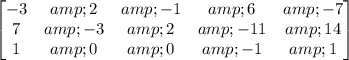
Applying row operations to solve for the reduced row-echelon form:

Step 1: Replace Row2 with Row2 + 2 * Row1 and Row3 with Row3 + 3 * Row1

`$$\begin{bmatrix}-3 & 2 & -1 & 6 & -7 \\1 & -7 & 0 & 1 & 0 \\0 & 0 & 0 & 0 & 4 \\\end{bmatrix}$$`

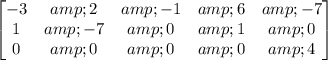
Step 2: Replace Row1 with (-1/3) * Row1

`$$\begin{bmatrix}1 & -2/3 & 1/3 & -2 & 7/3 \\1 & -7 & 0 & 1 & 0 \\0 & 0 & 0 & 0 & 4 \\\end{bmatrix}$$`

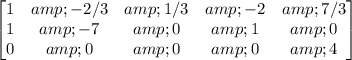
Step 3: Replace Row2 with Row2 - Row1

`$$\begin{bmatrix}1 & -2/3 & 1/3 & -2 & 7/3 \\0 & -11/3 & -1/3 & 3 & -7/3 \\0 & 0 & 0 & 0 & 4 \\\end{bmatrix}$$`

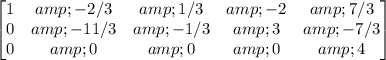
Step 4: Replace Row2 with (-3/11) * Row2

`$$\begin{bmatrix}1 & -2/3 & 1/3 & -2 & 7/3 \\0 & 1 & 1/11 & -9/11 & 7/11 \\0 & 0 & 0 & 0 & 4 \\\end{bmatrix}$$`

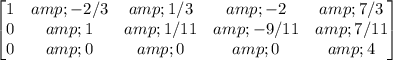
Step 5: Replace Row1 with Row1 + (2/3) * Row2

`$$\begin{bmatrix}1 & 0 & 5/33 & -5/33 & 25/33 \\0 & 1 & 1/11 & -9/11 & 7/11 \\0 & 0 & 0 & 0 & 4 \\\end{bmatrix}$$`

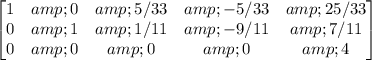
This matrix represents the system of equations in the reduced row-echelon form.

The solution is:

`$$\begin{align*}x_1 &= (25)/(33) + (5)/(33)x_3 - (5)/(33)x_4 \\x_2 &= (7)/(11) - (1)/(11)x_3 + (9)/(11)x_4 \\x_3 &= \text{free variable} \\x_4 &= \text{free variable} \\\end{align*}$$`