Question

A researcher wishes to estimate, with 99% confidence, the population proportion of adults who support labeling legislation for genetically modified organisms (GMOs). Her estimate must be accurate within 7% of the true proportion. (a) No preliminary estimate is available. Find the minimum sample size needed. (b) Find the minimum sample size needed, using a prior study that found that 82% of the respondents said they support labeling legislation for GMOs. (c) Compare the results from parts (a) and (b). (a) What is the minimum sample size needed assuming that no prior information is available? (Round up to the nearest whole number as needed.) n =

Answer 1

The minimum sample size needed, assuming no prior information is available, to estimate the population proportion of adults supporting labeling legislation for GMOs with 99% confidence and an accuracy of within 7% of the true proportion is approximately n = 645.

Explanation:

To calculate the minimum sample size needed without prior information, we use the formula for sample size in estimating population proportion: times p \times
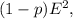`(1 - p)}{E^2}\right)\),` where
`\(Z\)`is the Z-score corresponding to the desired confidence level (99% in this case), \(p\) is the estimated proportion (0.5 is often used when there's no preliminary estimate), and is the margin of error (7% or 0.07).

For a 99% confidence level, the Z-score is approximately 2.576. Substituting these values into the formula, we get:

`\(n = \left((2.576^2 * 0.5 * (1 - 0.5))/(0.07^2)\right) = 644.97\)`

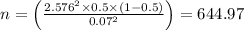
Rounding up to the nearest whole number, the minimum sample size needed without prior information is \(n = 645\).

This sample size ensures a 99% confidence level that the true population proportion falls within the range estimated by the sample, with a margin of error of 7%. It provides a robust estimate without relying on any preliminary data, ensuring a higher level of confidence in the findings regarding the support for GMO labeling legislation among adults in the population.