Question

Would you favor spending more federal tax money on the arts? Of a random sample of n1 = 213 women, r1 = 63 responded yes. Another random sample of n2 = 183 men showed that r2 = 60 responded yes. Does this information indicate a difference (either way) between the population proportion of women and the population proportion of men who favor spending more federal tax dollars on the arts? Use = 0.05.

Find (or estimate) the P-value. (Round your answer to four decimal places.)

Answer 1

To determine if there is a difference in the population proportion of women and men who favor spending more federal tax dollars on the arts, we can conduct a hypothesis test using the formula for two-sample proportions.

Step-by-step explanation:

To determine if there is a difference in the population proportion of women and men who favor spending more federal tax dollars on the arts, we can conduct a hypothesis test. The null hypothesis (H0) states that there is no difference, while the alternative hypothesis (Ha) states that there is a difference.

We can use the formula for two-sample proportions to calculate the pooled proportion (pooled p), which is used in the test statistic. The formula is:

pooled p = (r1 + r2) / (n1 + n2)

Using the given information, we can calculate:

pooled p = (63 + 60) / (213 + 183) =

pooled p = 123 / 396 =

Answer 2

The p-value (0.0009) is less than the chosen significance level α=0.05, we reject the null hypothesis. This suggests that there is evidence of a difference between the population proportions of women and men favoring spending more federal tax dollars on the arts.

To test if there is a difference between the population proportions of women and men who favor spending more federal tax dollars on the arts, we can use a two-sample z-test for proportions.

The null hypothesis
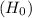`\left(H_0\right)` is that there is no difference between the population proportions, and the alternative hypothesis
`\left(H_1\right)` is that there is a difference.

Let
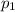`p_(1)` be the population proportion of women favoring spending on the arts,
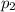`p_(2)` be the population proportion of men favoring spending on the arts.

The test statistic z is calculated as:

`z=\frac{\hat{p}_1-\hat{p}_2}{\sqrt{p(1-p)\left((1)/(n_1)+(1)/(n_2)\right)}}`

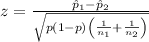
where
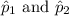`\hat{p}_1 \text { and } \hat{p}_2` are the sample proportions, p is the combined sample proportion,
`n_(1)` and
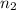`n_2}` are the sample sizes.

The combined sample proportion p is calculated as:

`p=(r_1+r_2)/(n_1+n_2)`

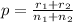
In this case:

`\begin{aligned}& \hat{p}_1=(r_1)/(n_1) \\& \hat{p}_2=(r_2)/(n_2)\end{aligned}`

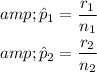
Given:

`\begin{array}{ll}n_1=213, & r_1=63 \\n_2=183, & r_2=60\end{array}`

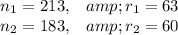
First, calculate the combined sample proportion p:

`p=(63+60)/(213+183)`

Now, calculate the test statistic z:

`z=\frac{(63)/(213)-(60)/(183)}{\sqrt{(123)/(396) *\left(1-(123)/(396)\right) *\left((1)/(213)+(1)/(183)\right)}}`

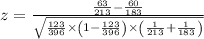
Calculate this expression to find the test statistic z.

Finally, find the p-value associated with this z value. The p-value is the probability of observing a test statistic as extreme as the one computed from the sample, assuming the null hypothesis is true. You can use a standard normal distribution table or a statistical software package to find the p-value.

Let's calculate the combined sample proportion p:

`p=(63+60)/(213+183)=(123)/(396)`

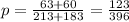
Now, let's calculate the test statistic z:

`\begin{aligned}& z \approx (0.2958-0.3279)/(√(0.1234 * 0.8766 *(0.0047+0.0055))) \\& z \approx (-0.0321)/(√(0.1234 * 0.8766 * 0.0102))\end{aligned}`

`\begin{aligned}& z \approx (-0.0321)/(√(0.0104 * 0.0102)) \\& z \approx (-0.0321)/(√(0.00010608)) \\& z \approx (-0.0321)/(0.010296) \\& z \approx-3.12\end{aligned}`

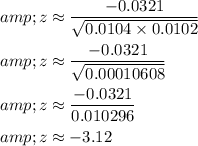
Now, we need to find the p-value associated with z=−3.12. Using a standard normal distribution table or a statistical software package, we find that the p-value is approximately 0.0009 (rounded to four decimal places).

Therefore, the p-value is 0.0009.