Question

Shen deposited $5000 into an account with a 6.4% annual interest rate, compounded quarterly. Assuming that no withdrawals are made, how long will it take for the investment to grow to $6145 ?

Do not round any intermedlate computations, and round your answer to the nearest hundredth.

Answer 1

We can use the compound interest formula to solve this problem:

`A=P(1+ (r)/(n) )^(nt)`

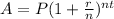
Where:

• A = the future value of the investment ($6145)
• P = the initial deposit ($5000)
• r = annual interest rate (6.4% or 0.064)
• n = number of times interest is compounded per year (quarterly, so 4)
• t = number of years

Substituting the given values into the formula:

`6145=5000(1+(0.064)/(4) )^(4t)`

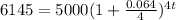
Now, we need to solve for t. Divide both sides by 5000 and then take the natural logarithm (ln) of both sides:

`ln((6145)/(5000) ) = 4tln (1+(0.064)/(4))`

Now, isolate t by dividing both sides by
`4 ln (1+(0.064)/(4) )`:

`t=(ln(6145)/(5000) )/(4ln(1+ (0.064)/(4) ))`

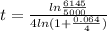
Now, plug in the values and calculate:

`t = (0.201943)/(4⋅0.015760) = 3.18`

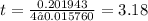
Rounded to the nearest hundredth, it will take approximately 3.18 years for the investment to grow to $6145.