Question

PLEASE HELP! I NEED by TODAY ! :(

Find an equation for the graph sketched below:
f(x) =

Answer 1

Answer:
`f(x)=3^(x+1)-1`

Explanation:

To solve this, we first need to know the parent function.

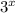`3^x` is the parent function of the equation.

The points in the parent function would be (0,1)
`3^0`=1, (1,3)
`3^1`=3, (2,9)
`3^2`=9 and so on and so forth. The asymptote is horizontal at y=0, meaning the values of x can come as close to y=0 as possible but never pass it.

Since the asymptote in the graph is at y=-1, the graph definitely moved down one. So our new equation is
`f(x)=3^x-1`.

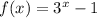Now, if we plug the values in, every point is one less, (0,0)
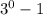`3^0-1`=0, (1,2)
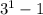`3^1-1`=2, (2,8)
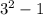`3^2-1`=8, (etc).

But that still doesn't match our graph. If we shift everything 1 unit to the left, the x values will change by being one less. So (-1,0)
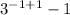`3^(-1+1)-1`=0, (0,2)
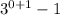`3^(0+1) -1`=2, (1,8)
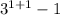`3^(1+1)-1`=8, (etc). This is since -1+1 is 0, and
`3^(0)` is 1 (any number to the 0 power is 1) and 1-1 is 0. That's why if x is -1, y is 0 in the equation
`f(x)=3^(x+1)-1`. That pattern continues with the other numbers, therefore we have our answer.

Hope that helped a lot.

:)