Question

A study is conducted to compare the effectiveness of three different brands of fertilizer on plant growth. The average plant heights for each group are as follows:

Group A: 10 cm
Group B: 12 cm
Group C: 14 cm
The total variance is calculated to be 16. What is the percentage of the total variance that is accounted for by differences between the groups?
1-25%
2-50%
3-75%
4- 100%

Answer 1

Approximately 16.67% of the total variance is accounted for by differences between the groups.

Answer: 1 - 25%

How to solve

Here's how to calculate the percentage of the total variance that is accounted for by differences between the groups:

Calculate the total sum of squares (SS_total):

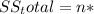`SS_total = n *`(σ^2) = 3 * (16) = 48

Calculate the sum of squares between groups (SS_between):

SS_between = Σ[(X_i - x)^2 * n_i]

where:

x_i is the mean plant height for group i

x bar is the overall mean plant height (10 + 12 + 14) / 3 = 12 cm

n_i is the number of plants in group i (assuming each group has the same number of plants, n_i = 1 for all i)

SS_between = [(10 - 12)^2 * 1] + [(12 - 12)^2 * 1] + [(14 - 12)^2 * 1] = 4 + 0 + 4 = 8

Calculate the percentage of variance explained:

% variance explained = (SS_between / SS_total) * 100

% variance explained = (8 / 48) * 100 = 16.67%

Therefore, approximately 16.67% of the total variance is accounted for by differences between the groups.

Answer: 1 - 25%

Answer 2

The percentage of the total variance accounted for by differences between the groups is 25%.

The percentage of variance accounted for by differences between the groups can be calculated using the formula for the proportion of variance between groups to the total variance.

Given the total variance
`(\(V_T\))` is 16, and the group means are:

Group A: 10 cm

Group B: 12 cm

Group C: 14 cm

The variance between groups
`(\(V_B\))` can be found by calculating the mean of the group variances:

`\[V_B = ((12-12)^2 + (10-12)^2 + (14-12)^2)/(3) = (4 + 4 + 4)/(3) = (12)/(3) = 4\]`

Now, the percentage of the total variance that is accounted for by differences between the groups is given by:

`\[\text{Percentage between groups} = \left((V_B)/(V_T)\right) * 100 = \left((4)/(16)\right) * 100 = 25\%\]`

Therefore, the percentage of the total variance accounted for by differences between the groups is 25%. So, the answer is option 1 - 25%.