Question

PLEASE HELP

Write the expression as a number in scientific notation.

the quantity 5.2 times ten to the fifth power end quantity times the quantity 1.5 times ten to the negative eighth power end quantity all divided by the quantity 2.5 times ten to the negative fourth power end quantity

4.2 × 10−7
4.2 × 107
3.12 × 10−1
3.12 × 101

Answer 1

The last option,
`3.12 * 10 ^(1)`

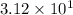
Explanation:

The expression given is:

`\rightarrow ((5.2 * 10^(5))(1.5 * 10^(-8)))/(2.5 * 10^(-4))`

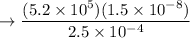
To simplify this expression, let's break it down step-by-step:

(1) First, let's multiply the numbers in the numerator:

`\Longrightarrow (5.2 * 10^(5))(1.5 * 10^(-8))`

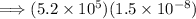
When you multiply numbers in scientific notation, you can multiply the decimal parts and then add the exponents of the powers of 10. So:

`\Longrightarrow (5.2 \cdot 1.5) * 10^(5+(-8))\\\\\\\\\Longrightarrow \boxed{7.8 * 10^(-3)}`

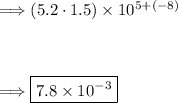
(2) Now, let's substitute this value into the numerator of the expression:

`\Longrightarrow (7.8 * 10^(-3))/(2.5 * 10^(-4))`

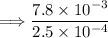
(3) To divide numbers in scientific notation, you divide the decimal parts and subtract the exponent of the divisor from the exponent of the dividend:

`\Longrightarrow \Big((7.8)/(2.5)\Big) * 10 ^(-3-(-4))\\\\\\\\\Longrightarrow 3.12 * 10 ^(-3+4)\\\\\\\\\Longrightarrow \boxed{3.12 * 10 ^(1)}`

`\therefore \boxed{\boxed{((5.2 * 10^(5))(1.5 * 10^(-8)))/(2.5 * 10^(-4))=3.12 * 10 ^(1)}}`

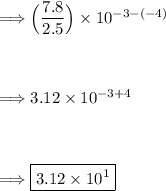
Thus, the last option is the correct answer choice.

`\hrulefill`

Additional information:

Scientific Notation: Scientific notation is a way of writing very large or very small numbers in a more compact and manageable form. It consists of a coefficient (a decimal number between 1 and 10) multiplied by a power of 10.

Properties of Exponents: Working with numbers in scientific notation involves applying the properties of exponents. The laws of exponents govern how to manipulate powers of numbers, and these properties are directly applicable when multiplying and dividing numbers expressed in scientific notation. Here's a list of exponent properties:

`\boxed{\left\begin{array}{ccc}\text{\underline{Properties of Exponents:}}\\\\1.\ a^0=1\\\\2.\ a^m * a^n=a^(m+n)\\\\3.\ a^m / a^n \ ((a^m)/(a^n) )=a^(m-n)\\\\4.\ (ab)^m=a^mb^m\\\\5.\ (a/b)^m=a^m/b^m\\\\6.\ (a^m)^n=a^(mn)\\\\7.\ a^(-m)=1/a^m\\\\8.\ a^(m/n)=(\sqrt[n]{a} )^m\end{array}\right}`

Multiplying Numbers in Scientific Notation: When you multiply numbers in scientific notation, you focus on two main components: the coefficient (the decimal part of the number) and the exponent (the power of 10).

For example, let's consider two numbers:
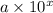`a * 10^(x)` and
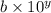`b * 10^y`, where 'a' and 'b' are coefficients and 'x' and 'y' are exponents. The product of these two numbers is:

`\Longrightarrow ab * 10^(x+y)`

Here, you multiply the coefficients together and add the exponents to get the result in scientific notation.

Dividing Numbers in Scientific Notation: When you divide numbers in scientific notation, you again focus on the coefficient and exponent components.

For example, let's consider two numbers:
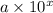`a * 10^(x)` (dividend) and
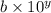`b * 10^y` (divisor), where 'a,' 'b,' 'x,' and 'y' are as defined before. The result of dividing the dividend by the divisor is:

`\Longrightarrow (a)/(b) * 10^(x-y)`

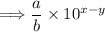
Here, you divide the coefficients and subtract the exponent of the divisor from the exponent of the dividend to get the result in scientific notation.

Answer 2

`\boxed{\sf 3.12 * 10^1}`

Explanation:

Writing the expression as a number in scientific notation.

`\sf (5.2*10^5*1.5*10^(-8))/(2.5*10^(-4))`

In order to write the expression in scientific notation, we can follow these steps:

Separate the numbers from the powers of 10 in the expression as follows:

`\sf (5.2*10^5*1.5*10^(-8))/(2.5*10^(-4)) = (5.2*1.5)/(2.5) * (10^5*10^(-8))/(10^(-4))`

Multiply the numbers together, we get

`\sf 3.12 * (10^5*10^(-8))/(10^(-4))`

Add the powers of 10 together using

`\textsf{Product of powers formula: }\boxed{\sf a^m \cdot a^n = a^(m+n)}`, we get

`\sf 3.12 * (10^(5-8))/(10^(-4))`

`\sf 3.12 * (10^(-3))/(10^(-4))`

Subtract the power of 10 using '

`\textsf{Quotient of powers formula:}\boxed{\sf (a^m)/(a^n) = a^(m-n)}`, we get

`\sf 3.12 * 10^(-3-(-4))`

`\sf \sf 3.12 * 10^(-3+4)`

`\sf 3.12 * 10^1`

Therefore, the expression in scientific notation is
`\boxed{\sf 3.12 * 10^1}`