Question

You are playing a game that has a spinner. It will either come up 1, 2, 3, or 4. They all have an equal likelihood of occurring. You spin it 4 times and add the numbers together. What is the expected value and what is the variance of the sum?

Answer 1

The expected value of the sum of four spins of the spinner is 2.5. The variance of the sum is 0.625.

Step-by-step explanation:

To find the expected value of the sum of four spins of a spinner with numbers 1, 2, 3, and 4, we need to calculate the average sum based on the probabilities of each number appearing. The expected value is found by multiplying each number by its probability and adding up the results. In this case, since all numbers have an equal likelihood of occurring, the probability of each number is 1/4. Therefore, the expected value is (1 * 1/4) + (2 * 1/4) + (3 * 1/4) + (4 * 1/4) = 2.5. So the expected value of the sum is 2.5.

To find the variance of the sum, we first need to find the squared differences between each number and the expected value. Then we multiply each squared difference by its probability and add up the results. The variance formula is Var(X) = E[(X - E(X))^2]. In this case, the squared differences are (1-2.5)^2, (2-2.5)^2, (3-2.5)^2, and (4-2.5)^2. The probabilities are all 1/4. Calculating the variance, we get (1/4)*(1.5^2) + (1/4)*(-0.5^2) + (1/4)*(0.5^2) + (1/4)*(1.5^2) = 0.625. So the variance of the sum is 0.625.

Answer 2

The expected value is 2.5, and the variance of the sum is 3.375.

Step-by-step explanation:

The expected value is the sum of the products of each outcome and its probability. Since all the outcomes (1, 2, 3, and 4) have an equal likelihood of occurring (1/4), the expected value is:

Expected value = (1/4) x 1 + (1/4) x 2 + (1/4) x 3 + (1/4) x 4

= 1/4 + 1/2 + 3/4 + 1

= 2.5

The variance of the sum can be calculated by finding the variance of each individual outcome and summing them. The variance of each outcome is given by:

`Var(X) = (x - E(X))^2 x P(X)`

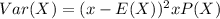
where x is the outcome, E(X) is the expected value, and P(X) is the probability of that outcome happening.

The variance of the sum is:

Var(sum) = Var(1) + Var(2) + Var(3) + Var(4)

`= (1 - 2.5)^2 x (1/4) + (2 - 2.5)^2 x (1/4) + (3 - 2.5)^2 x (1/4) + (4 - 2.5)^2 x (1/4)`

`= (1.5)^2 x (1/4) + (0.5)^2 x (1/4) + (0.5)^2 x (1/4) + (1.5)^2 x (1/4)`

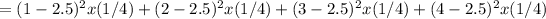
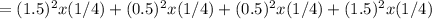
= 3.375