Question

The diagram shows a circle, radius rcm and minor sector angle x². The perimeter of the major sector is three times the perimeter of the minor sector. 90 (A-2) Show that x=​

Answer 1

`x =(90(\pi -2))/(\pi)`

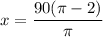
Explanation:

The given diagram shows a circle, with radius r cm and minor sector angle x°.

A sector is a portion of a circle enclosed by two radii and the corresponding arc between them. Sectors are often categorized into major and minor sectors based on the size of the central angle that defines them.

• A major sector has a central angle greater than 180°.
• A minor sector has a central angle less than 180°.

The perimeter of a sector is the sum of two radii and the arc length.

Therefore, the formula for the perimeter of a sector is:

`\large\boxed{P=2r+(2\pi r\theta )/(360^(\circ))}`

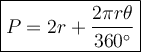
where:

• r is the radius.
• θ is the measure of the central angle (in degrees).

As the central angle of the minor sector is x°, this means the central angle of the major sector is (360 - x)°, since angles around a point sum to 360°.

Therefore, we can create two equations for the perimeter of the minor and major sectors of the given circle:

`\textsf{Perimeter of minor sector}=2r+(2\pi rx^(\circ))/(360^(\circ))`

`\textsf{Perimeter of major sector}=2r+(2\pi r(360-x)^(\circ))/(360^(\circ))`

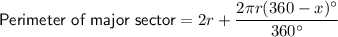
We are told that the perimeter of the major sector is three times the perimeter of the minor sector. Therefore:

`\begin{aligned}3\cdot\textsf{Perimeter of minor sector}&=\textsf{Perimeter of major sector}\\\\3\left(2r+(2\pi rx^(\circ))/(360^(\circ))\right)&=2r+(2\pi r(360-x)^(\circ))/(360^(\circ))\end{aligned}`

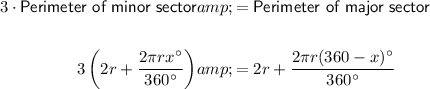
Solve the equation for x.

Expand the brackets on the left side of the equation:

`6r+(6\pi rx^(\circ))/(360^(\circ))=2r+(2\pi r(360-x)^(\circ))/(360^(\circ))`

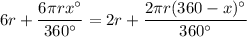
Rewrite 6r and 2r as equivalent fractions, where 360 is the denominator:

`(2160r)/(360)+(6\pi rx)/(360)=(720r)/(360)+(2\pi r(360-x))/(360)`

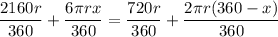
Multiply both sides of the equations by 360:

`2160r+6\pi rx=720r+2\pi r(360-x)`

Expand the brackets on the right side:

`2160r+6\pi rx=720r+720\pi r -2 \pi rx`

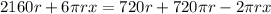
Add 2πrx to both sides, and subtract 2160r from both sides:

`8\pi rx=720\pi r -1440r`

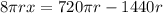
Divide both sides of the equation by 8r:

`\pi x =90\pi -180`

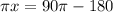
Factor out 90 from the right side of the equation:

`\pi x =90(\pi -2)`

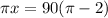
Divide both sides of the the equation by π:

`x =(90(\pi -2))/(\pi)`

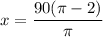
Hence, we have shown that:

`\large\boxed{x =(90(\pi -2))/(\pi)}`