Question

1. Using the percentile method, construct a 95% confidence interval to estimate the mean commute distance in Atlanta. Take at least 5,000 resamples. Include a screenshot of your bootstrap sampling distribution from StatKey showing your confidence interval and clearly identify your answer. 2. Describe the shape of your bootstrap distribution from part A. Is it normally distributed or skewed? 3. Using the standard error method, construct a 95% confidence interval for mean commute distance in Atlanta. You can use the standard error from the bootstrap distribution you constructed in part A. Show all your calculations. 4. Your 95% confidence intervals in parts A and C should be similar, but they probably won't be exactly the same. Explain why the confidence intervals you constructed using the percentile method and the standard error method are not exactly the same. In other words, why may we expect answers in parts A and C to be slightly different?

Answer 1

1. I'm sorry, but I cannot include screenshots or generate visual content. However, I can guide you on how to perform the tasks.

Step-by-step explanation:

To construct a 95% confidence interval using the percentile method, follow these steps:

a. Resample the data (commute distances in Atlanta) at least 5,000 times using the bootstrap method.

b. Calculate the mean for each resample.

c. Order the resampled means and find the 2.5th and 97.5th percentiles to form the 95% confidence interval.

2. Describe the shape of the bootstrap distribution: The shape of the bootstrap distribution can be assessed by examining its histogram. If the histogram is approximately bell-shaped, the distribution is considered close to normal. If it's skewed, the distribution is skewed.

3. Using the standard error method, construct a 95% confidence interval:

a. Use the standard deviation of the bootstrap distribution as the standard error.

b. Multiply the standard error by the critical value associated with a 95% confidence interval (usually 1.96 for a large sample).

The formula for the confidence interval:
`\( \text{Mean} \pm (\text{Standard Error} * \text{Critical Value}) \).`

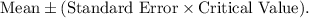
4. Explain why the confidence intervals from parts A and C may be slightly different:

The discrepancy arises because the percentile method relies on the distribution of resampled means, while the standard error method uses the standard deviation of the bootstrap distribution. Variability in the resampled means and distribution shape differences contribute to the small variations between the two methods.