Question

The amount of syrup that people put on their pancakes is normally distributed with mean 65 mL and standard deviation 8 ml. Suppose that 12 randomly selected people are observed pouring syrup on their pancakes. Round all answers to 4 decimal places where possible. a. What is the distribution of X? X - NC b. What is the distribution of x? - Nd c. If a single randomly selected individual is observed, find the probability that this person consumes is between 67.8 mL and 69.6 mL. d. For the group of 12 pancake eaters, find the probability that the average amount of syrup is between 67.8 mL and 69.6 mL. e. For part d), is the assumption that the distribution is normal necessary? i) NO ii) Yes

Answer 1

a. The distribution of X is normal with a mean of 65 mL and a standard deviation of 8 mL. b. The distribution of x is normal with a mean of 0 and a standard deviation of 1. c. The probability of a single randomly selected individual consuming between 67.8 mL and 69.6 mL can be calculated using the standard normal distribution.

Step-by-step explanation:

a.

The distribution of X is a normal distribution with a mean of 65 mL and a standard deviation of 8 mL, denoted as X ~ N(65, 8).

b.

The distribution of x is a normal distribution with a mean of 0 and a standard deviation of 1, denoted as x ~ N(0, 1).

c.

To find the probability that a single randomly selected individual consumes between 67.8 mL and 69.6 mL, we need to use the standard normal distribution.

1. Calculate the z-scores for the lower and upper values: z1 = (67.8 - 65) / 8 and z2 = (69.6 - 65) / 8.
2. Look up the corresponding cumulative probabilities for the z-scores using a standard normal distribution table or calculator.
3. Subtract the lower cumulative probability from the upper cumulative probability to find the desired probability.

d.

To find the probability that the average amount of syrup for a group of 12 pancake eaters is between 67.8 mL and 69.6 mL, we can use the central limit theorem and treat the sample mean as the average amount of syrup for each individual in the group. The distribution of sample means will be approximately normal with a mean equal to the population mean (65 mL) and a standard deviation equal to the population standard deviation divided by the square root of the sample size (8 mL / sqrt(12)).

Following the same steps as in part c, calculate the z-scores for the lower and upper values using the sample mean and standard deviation, and then find the desired probability using the standard normal distribution.

e.

The assumption that the distribution is normal is necessary for part d) because we are using the central limit theorem, which requires a normal population distribution. If the distribution is not normal, the central limit theorem may not apply and the result may not be accurate.

Answer 2

The distribution of syrup amounts follows a normal distribution, and for a sample mean of 42 people, the assumption of normality is valid, allowing us to calculate probabilities accurately.

a. The distribution of X for a single observation of syrup poured on pancakes follows a normal distribution with a mean of 64 mL and a standard deviation of 9 mL. So,
`\(X \sim \mathcal{N}(64, 9^2)\).`

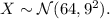
b. The distribution of
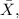`\(\bar{X}\),` the sample mean for a group of 42 individuals, also follows a normal distribution.

For the sample mean, the mean
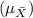`(\(\mu_{\bar{X}}\))` remains the same as the population mean (64 mL), and the standard deviation
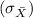`(\(\sigma_{\bar{X}}\))` is calculated as
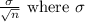`\((\sigma)/(√(n))\) where \(\sigma\)` is the population standard deviation and n is the sample size.

Therefore,
`\(\bar{X} \sim \mathcal{N}\left(64, (9)/(√(42))\right)\).`

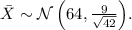
c. To find the probability that a single randomly selected individual consumes between 65.9 mL and 67 mL, we'll use the Z-score formula and then find the probability using the standard normal distribution:

`\[Z = (X - \mu)/(\sigma)\]`

Where X is the value (67 mL),
`\(\mu\)` is the mean (64 mL), and
`\(\sigma\)` is the standard deviation (9 mL).

`\[Z_(67) = (67 - 64)/(9) = (3)/(9) = 0.3333\]`

Now, we find the corresponding probabilities using a standard normal distribution table or calculator.

`\[P(65.9 < X < 67) = P(0 < Z < 0.3333)\]`

d. For the group of 42 pancake eaters, finding the probability that the average amount of syrup is between 65.9 mL and 67 mL involves using the properties of the sample mean distribution:

`\[P(65.9 < \bar{X} < 67) = P\left(\frac{65.9 - \mu_{\bar{X}}}{\sigma_{\bar{X}}} < Z < \frac{67 - \mu_{\bar{X}}}{\sigma_{\bar{X}}}\right)\]`

Substitute the values of
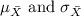`\(\mu_{\bar{X}}\) and \(\sigma_{\bar{X}}\)` into the formula and use the Z-score approach similar to part c to find this probability.

e. For part d), the assumption that the distribution is normal is necessary due to the central limit theorem, which states that the sample mean of a sufficiently large sample size from any population will be approximately normally distributed. Therefore, with a sample size of 42 (which is considered relatively large), the normality assumption holds for the sample mean distribution.